Опробована методика функционального моделирования энергетического пространства состояния многоструктурного объекта. Состояние объекта оценивается с помощью обобщенного интегрального параметра. Обобщенный параметр получен на основе идентификации априорных и экспериментальных данных на лабораторно-вычислительном комплексе.
Получены новые экспериментальные зависимости, связывающие обобщенный интегральный показатель с потоками, силами и свойствами разных по назначению структур.
По своей значимости результаты аналогичны решению комплекса дифференциальных нелинейных уравнений высокого порядка. Искомые решения получены в алгебраическом виде. Что затруднительно сделать даже при наличии мощных ЭВМ.
Экспериментальные выходные параметры в виде безразмерных удельных потоков энергии связаны с термодинамическими, геометрическими, временными параметрами систем.
Функций коэффициентов неравновесности позволяют сравнивать затраты энергии для каждой структуры и выбирать их оптимальные значения.
Выходные траектории функционала нелинейны, что указывает на свойства неравновесности и необратимости исследуемых процессов.
Процедуры получения выходных траекторий итерационные и открыты для варьирования из условий минимума отклонения удельной энергии от нормированных значений.
Энергетическое пространство состояния разнородной структуры удовлетворяет условиям однозначности и целевой функции полезности сформулированных краевых энергетических задач.
Результаты натурного и численного экспериментов косвенным путем сопоставлены с данными других исследований.
Предлагаемая методика функционального моделирования состояния структуры увеличивает скорость восприятия материала и поэтому применима в междисциплинарных исследованиях, в том числе для обучения.
Методика создана на основе методов системного анализа, неравновесной, феноменологической термодинамики, синергетики численного и натурного экспериментов.
Энтропия как калорический параметр широко используется для описания теплоэнергетических процессов. Основополагающими в этом отношении являются работы М.П. Вукаловича, И.И. Новикова, А.И. Андрющенко, Л.И. Седова, В.М. Бородянского, Д.П. Гохштейна, и др. [5, 6, 7]. Понятие энтропии широко принято в эксергетических расчетах теплотехнических систем [13]. В работах А.В. Дмитриенко, В.Г. Попова наиболее полно проведён системный анализ существующих законов неравновесной термодинамики, которая использует для построения своих моделей феноменологические уравнения теории энтропии [8].
Из обзора следует, что энтропийные постановки хорошо приспособлены для оценки состояния исследуемой диссипационной структуры. Сформулированные в [9, 10, 11] основные законы энергоэнтропики функционально увязывают движущие силы, свойства, потоки вещества и энергии рабочего тела. Действия сил и потоков в условиях недалеких от равновесия указывают на справедливость феноменологических законов Ома, Дарси, Фурье и т.д. Проверка уместности их использования в связи с ростом интенсивности потребления энергии становится все актуальнее, и должна проводиться в каждом конкретном случае экспериментальным путем с установлением связей функционального характера (1)
S = f [потоки, силы ,свойства, геометрические параметры]. (1)
Для каналов круглого и прямоугольного сечений с различными свойствами движущихся теплоносителей зависимость (1) имеет вид с дробными параметрами [12, 14], (2), (3), (4):
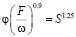, (2)
где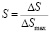 
– безразмерный критерий термодинамического подобия; j – критерий Стантона, F – поверхность теплообмена, м2; w – площадь поперечного сечения канала, м3;
,
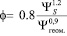где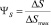 
,
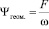. (3)
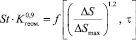. (4)
В функционале (4) энтропийный параметр содержится в неявном виде. Однако доказана его корреляция в функциональных связях между тепловыми потоками, свойствами теплоносителя, временем течения процесса [7, 12].
Для доказательства существования «обобщенного параметра» субъект получает новые зависимости в виде «обобщенного параметра» состояния для новых условий энергообмена на новых лабораторных вычислительных комплексах.
Ниже представлен состав комплекса, алгоритмическая структура и методика обработки результатов исследований рис. 1.
Для достижения цели эксперимент проведен на нескольких установках типа источник-приемник энергии (ИПЭ). В каждой паре ИПЭ изучается свой набор энергопреобразований: условия взаимодействия газового инфракрасного излучателя с металлической пластиной (ИГИ-МП), электрического инфракрасного излучателя с поверхностью из кирпичной стенки (ЭИИ-КС), электрического тепловыделяющего элемента через изоляционный материал и цилиндрическую металлическую поверхность с окружающей средой (Э-ТВЭ-ОС).
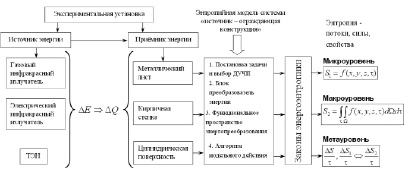
Рис. 1. Системная идентификация «обобщенного» структурного параметра
Набор установок и приборные возможности позволяют провести экспериментальные исследования для основных явлений нестационарной теплопередачи теплоты теплопроводностью, конвекцией, излучением.
На рис. 1 представлена обязательная последовательность действий для получения результатов: постановка краевой задачи в виде системы дифференциальных уравнений в частных производных; рассмотрение каждой структуры в образе «обобщенного преобразователя энергии»; формирование структуры в терминах «пространства состояния»; построение алгоритма «конечного действия»; в априорную составляющую входят законы энергоэнтропики [15, 20]; апостериорную – результаты экспериментальных исследований; анализ полученного материала и его математическая обработка представлена в трех иерархических уровнях. [15].
В процессе системного изучения априорной информации выявляется структура объекта и ее параметры.
Структуризация термодинамической системы подразумевает совокупность блоков [15, 18] «преобразователей энергии». Блок преобразователь энергии представлен на рис. 2. Структура отражает в общем виде характерный потоковый баланс энергии и массы для условий существования объекта: семи потоковых форм, двух типов энергопреобразований, наличия трех рабочих тел.
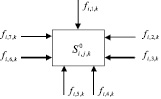
Рис. 2. Модель – блок «преобразователь разнородной энергии» типа «источник – приёмник энергии»
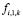– электрической энергии,
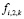– естественная конвекция,
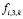– вынужденная конвекция,
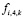– теплопроводность,
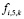– инфракрасное излучение,
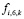– топливо (газ).
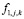– трансформатор энергии,
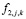– преобразователь энергии,
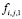– жидкость,
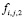– воздух,
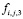– твёрдое тело.
Характеристические данные в таком виде позволяют субъекту строить функциональные зависимости 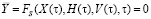(5):
, (5)
состояния системы.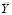 
– вектор траектории выходных параметров. X, H, V, – множества для векторов входных, внутренних, внешних параметров:
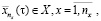
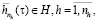
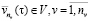. (6)
Параллельно с созданием функциональной записи, формируются условия краевой задачи в виде систем алгебраических и дифференциальных уравнений второго порядка в частных производных. Оценивается возможность решения такой системы численными методами. В случае большой нелинейности предпочтение отдается эксперименту, решаются инверсная и обратные задачи при известных из эксперимента граничных условиях рабочих тел участвующих в энергообмене.
Реализация численных процедур в любом случае нужна для определения градиентных или дивергентных характеристик соответствующих скалярных и векторных полей.
Для удобства классификации решаемых или нужных для решения задач результаты систематизированы на трех иерархических уровнях их представления. Как правило, после обработки экспериментальных данных нестационарное скалярное поле описывается в виде функции двух и или трех переменных 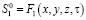(7).
. (7)
Макроуровневое описание модели(7) требует получения функции (8). Для этого (7) интегрируется по объему, поверхности или времени, в зависимости от цели поставленной задачи:
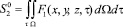. (8)
Уравнения (9) дают потоковые переменные, которые удобно сопоставлять между собой, а значит определять энергетические характеристики структур типа 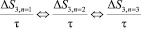(9).
. (9)
Схема экспериментальной установки, реализует модельное силовое состояние процесса теплопроводности в металлическом листе (рис. 3,а), кирпичной стенке (рис. 3,б), двухслойном цилиндрическом теле (рис. 3,в).Условия принуждения формируются от газового топливного инфракрасного излучателя белого типа, электрического инфракрасного излучателя и тепловыделяющего элемента под действием электрического тока.
Регулирование мощности источников теплоты позволяет реализовывать условия переключения с одного силового режима на другой и тем самым формировать переходные и нестационарные процессы в материале изделий. Предусмотрена система «аналог код» для передачи и выработки цифрового сигнала на компьютер.
Экспериментальная установка как комплекс источников и приемников энергии [4, 20] изображена на рис. 3.
а б в
Рис. 3. Структурное отражение лабораторно-вычислительного комплекса: а – (ИГИ-МП) – инфракрасный газовый излучатель, металлическая пластина, система аналог код с термопарами и компьютером. б – (ЭИИ-КС) –электрический инфракрасный излучатель, кирпичная стенка, система аналог код с компьютером; в – (ЭН-ЦТ)-электрический нагреватель с изоляцией и цилиндрической оболочкой, система аналог код и компьютер
Макроуровневый функционал вида (9) получен после интегрирования поля энтропий по объёму кирпичной стенки рис. 3б.
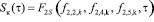(10)
Управление через лучистый поток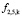 
позволяет осуществлять воздействие на поле энтропии. На рис. 4 показано развитие интегрального энтропийного поля во времени в четырех координатных точках сечения кирпичной стенки.
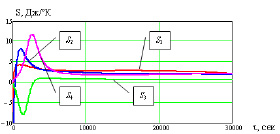
Рис. 4. Макроуровневые потоки S1, S2, S3, S4 при x = 0.01, 0.035, 0.065, 0.09 м
Энергетическое состояние сформировано на основе модели процесса теплопроводности. Поскольку другие составляющие (лучистая и конвективная) при малом уровне температур незначительно влияли на общий уровень энергообмена.
В первой задаче прим малой толщине пластины и быстрого прогрева ее по толщине основное внимание обращено решению задачи естественной конвекции.
Измерения температур и скоростей проведены термопарами и термоанемометрами.
Использование методов интерполяции и конечноразностной аппроксимации измеренных значений теплоносителя позволила найти температурные поля и потоки теплоты в движущейся воздушной среде. Отношение полей потоков и температур позволили определить поля локальной энтропии, рис. 5.
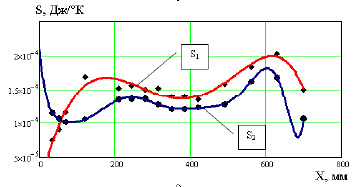
Рис. 5. Микроуровневые представления энтропийных конвективных потоков воздуха около пластины:1 – 15 мм от пластины; 2 – 25 мм от пластины
Траектория развития функционала после интегрирования поля энтропий по объёму пограничного слоя имеет вид
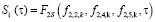, (10)
где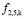 
принуждающее воздействие (11).
В наиболее общей постановке проведены экспериментальные исследования для задачи рис. 6,в.
На рис. 6,А,В показаны силовые характеристики поля механической и термической форм движения энергии в условиях естественной конвекции около цилиндра. Синим цветом (рис. 6,С) представлены расчётные скорости, красным – экспериментальные данные. Анализ полей показал, что в зоне малых скоростей экспериментальные и расчетные данные совпадают. С увеличением w от 0,3 до 1,8 м/с погрешность расчётных и экспериментальных данных достигает 46 %.
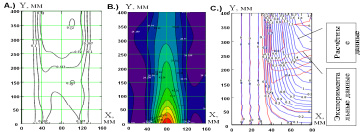
Рис. 6. Силовые поля термической и механической форм движения энергии в условиях естественной конвекции
Методами теории поля в движущемся потоке воздуха найдены касательные напряжения и плотности потоков теплоты.
На рис. 7 представлены экспериментальные нестационарные поля температур в цилиндрическом теле.
После перехода на макроуровневый вид представления тепловой и механической форм энергии определены функции энтропии в тепломеханической и теплопроводной частях объекта. А затем и суммарная величина удельной энергии для всей установки. Для цилиндрического тела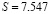 
Дж/°К., механическая составляющая в пограничном слое 
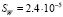Дж/°К., термическая составляющая пограничном слое 
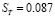Дж/°К.
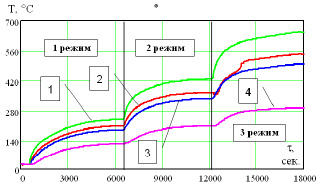
Рис. 7. Силовые термические характеристики теплопроводности в теле на 3-х режимах: 1 – температура ТЭНа, 2 – температура вещества на глубине 12 мм, 3 – температура вещества на глубине 6 мм, 4 – температура поверхности
Удельная обобщенная энергетическая характеристика системы за время ее работы составила
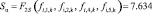Дж/°К. (12)
Уравнение (12) указывает на получение единого энергетического показателя в виде воспроизводства «обобщенной энтропии», характеризующего суммарное энергетическое состояние многоструктурной системы. Структура состоит из энергии присутствующей в формах «гидравлического» и «теплового» пограничного слоев, «теплопроводности» цилиндрического тела.
Разница в энергетическом состоянии системы на двух режимах ее работы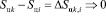 
, где k и i режимы работы, дает возможность субъекту сохранять интервал оптимального управления.
На рис. 8 представлены потоковые макроуровневые функции воспроизводства обобщенной энтропии в разных структурах (ЭИИ-КС) и (Э-ТВЭ-ОС).
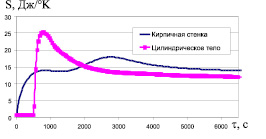
Рис. 8. Макроуровневое воспроизводство потоков энтропии различными теплотехническими структурами
Графики на рис. 8 построены на основе третьего закона энергоэнтропики (8) и позволяют сравнивать меняющийся во времени «обобщенный энергетический показатель» двух разных структур, который указывает на состояния этих энергетических структур. Динамика изменения позволяет вести оценку количества и качества энергии требуемой для термодинамических процессов.
Попытка обобщения полученных результатов на целый класс объектов с помощью критэриальной формулы (4) дала ряд функций рис. 9 при n = –2.05 – для цилиндрической металлической поверхности, n = –0.71 – для кирпичной стенки достаточно близко расположенные от области значений представленных другими авторами. Из рис. 9 следует, что разные по своему принципу работы тепловые системы описываются графиками с разбросом экспериментальных данных в 20 %. А формула (4) указывает на возможность управления энергетическими ресурсами трёх рассматриваемых структур. Связь энтропийных, потоковых, геометрических критериев позволяет наглядно демонстрировать на одном графике особенности и направление изменения «обобщенной энергии» в разных теплотехнических системах.
Такого рода результаты дают основание для построения параметрических номограмм, для групповой структуры, в которой «обобщенный относительный энтропийный критерий» замыкает на себя относительные «силы», «потоки», «свойства» исследуемой структуры. На рис. 10 раскрыт функционал (13) для системы «б» рис. 3.
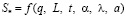, (13)
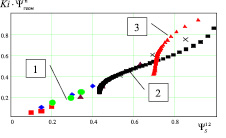
Рис. 9. Сравнение энтропийного представления для разных производственных объектов:1 – авторы по формулам (2, 3, 4), 2 – цилиндрическая ограждающая поверхность,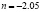
, 3 – кирпичная ограждающая поверхность,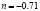 
где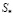 
– безразмерная энтропия системы; 
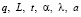– соответственно безразмерные плотность теплового потока от источников энергии разной мощности: 1 – 1 кВт, 2 – 2 кВт, 3 – 3 кВт; геометрический параметр, температура, коэффициент теплоотдачи, коэффициент теплопроводности и температуропроводности.
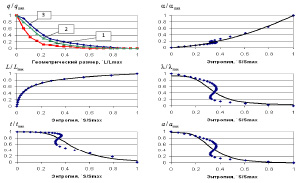
Рис. 10. Энтропийный функционал и его функции
Использование построенных номограмм освобождает исследователя множество раз пересчитывать системы нелинейных равнений для разных граничных условий в заданной области определения рабочих функций. Как следствие напрашивается вывод, что макроуровневое энтропийное представление удельного энергетического состояния структуры позволяет находить условия оптимального управления и функционирования объекта путем контроля минимизации отклонений воспроизводства энтропии (8), [20]. Для примера построим функционал (13), который позволяет записать, а затем и найти практически все параметры системы через связь «обобщенной суммарной энтропии» системы и входящих в нее структур. Функциональные зависимости, раскрывающие функционал (14) для двух структур показаны на рис (11).
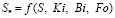, (14)
где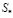 
– безразмерная суммарная энтропия двух систем; 
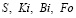– безразмерные параметры: энтропия одной из систем; критерий Кирпичёва; Критерий Био; время соответственно.
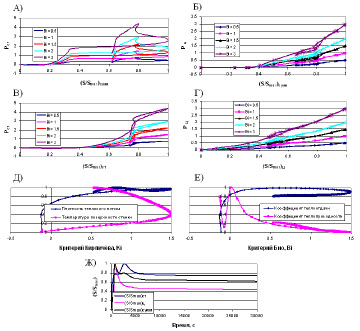
Рис. 11. Функциональные решения, связывающие в термодинамической системе через энтропийные критерии потоки, силы и свойства двух структур
На рис. 11 показаны следующие функциональные зависимости в виде произведений: А –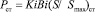 
критериев Кирпичёва, Био, энтропийного критерия от суммарной безразмерной энтропии для системы (ЭИИ-КС); Б – 
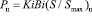Кирпичёва, Био, энтропийного критерия от суммарной безразмерной энтропии для системы (ЭН-ЦТ); В, Г – указывают на потоковые связи для кирпичной и цилиндрической стенок;. Д – функция связи безразмерных температур поверхности и плотности теплового потока с критерием Кирпичёва;. Е –связи безразмерных коэффициентов теплоотдачи, теплопроводности и критерия Био. Ж – связи безразмерной энтропии системы с реальным временем процесса. «Склеивание» двух структур в неравновесной термодинамической системе по параметру «суммарная безразмерная энтропия» позволяет определять параметры связи любого блока структуры. На рис. 11,А,Б экстремумы функций соответствуют характерному изменению свойств структуры и системы. Алгоритм работы с графиками рис. 11 требует по заданным значениям безразмерной энтропии и числа Bi, определить критерий Ki. Из графиков Д и Е по значениям Ki и Bi находятся свойства рабочих тел, плотности тепловых потоков, температур, коэффициенты теплопроводности, теплоотдачи. По Ж определяется реальное время процесса, по А доля энергии, которую необходимо затратить на прогрев кирпичной стенки в зависимости от общей суммарной энергии всей системы в целом.
Библиографическая ссылка
Игонин В.И., Белянский Д.А. Оценка обобщенного энергетического состояния нескольких теплотехнических систем // Современные наукоемкие технологии. – 2013. – № 5. – С. 46-54;URL: https://top-technologies.ru/ru/article/view?id=31798 (дата обращения: 26.12.2024).