Развитие средств обработки данных, используемых в процессе принятия управленческих решений, стимулирует расширение и совершенствование методов и алгоритмов построения математических моделей исследуемых объектов. Естественное стремление получения наилучшего результата предполагает системный подход к объекту управления с учетом всех возможных альтернатив. Практически любое управленческое решение – это решение на основе некоторого выбранного критерия с учетом имеющихся ограничений. Математическое описание подобной задачи позволяет использовать современные математические алгоритмы и специализированное программное обеспечение для выработки оптимального решения.
Алгоритмы и математические методы поиска оптимальных решений хорошо изучены и успешно применяются для управления как техническими объектами, так и для решения разнообразных задач микро- и макроэкономики [1]. Математическая модель исследуемого объекта, на основании которой осуществляется оптимизация, является важнейшим инструментом исследования и управления, и от того, насколько точно она отражает реальную действительность, в значительной мере зависит качество управления. С другой стороны, любая модель в конечном счете является упрощением, и при выборе управленческого решения необходимо это учитывать. При разработке и дальнейшем использовании математических моделей исследователь сталкивается с рядом неопределенностей, вызванных в первую очередь неучтенными в модели факторами. Влияние этих факторов приводит к появлению случайной составляющей модели и, как следствие, заставляет использовать при моделировании методы математической статистики и регрессионного анализа [2].
На стадии принятия управленческих решений проявляется еще один вид неопределенности, получивший название «многокритериальная неопределенность». Природа такой неопределенности кроется в желании обеспечить оптимальные значения по ряду показателей, которые далее будем называть критериями. Проблема заключается в том, что, как правило, достижение оптимума одновременно по всем критериям недостижимо в силу их противоречивости. Применение скалярных методов оптимизации в такой ситуации не снимает возникшую неопределенность. Исследованию моделей и методов многокритериальной оптимизации посвящено достаточно много как теоретических работ [3], так и примеров их практического использования [4, 5]. Большое значение для понимания принципов построения методов многокритериальной оптимизации имело сформулированное в начале XX в. испанским экономистом Парето понятие эффективных решений. С точки зрения Парето, к эффективным решениям можно отнести любое решение задачи многокритериальной оптимизации при условии, что его нельзя улучшить одновременно по двум или более критериям. Дальнейшее развитие теории и практики многокритериальной оптимизации сводилось к разработке компромиссных методов выбора решения.
Среди отечественных ученых значительный вклад в развитие методов многокритериальной оптимизации принадлежит В.В. Подиновскому. В монографии [6] и других теоретических работах этого ученого раскрываются основные идеи и подходы при выборе оптимального решения в условиях многокритериальной неопределенности. Большинство рассматриваемых подходов основано на ранжировании критериев и выборе решения на основе выделенных приоритетов. Среди этой группы методов можно выделить метод анализа иерархий (МАИ), предложенный Т. Саати [7], который рассматривает различные варианты развития методов ранжирования с учетом специфики исследуемых задач. К этому же классу методов относятся алгоритмы формирования глобального критерия на основе весовых коэффициентов критериев и сведение задачи к скалярному варианту с одним критерием. При возможности выделения основного критерия в ряд алгоритмов оптимизации менее важные критерии учитываются как ограничения в задаче оптимизации.
В данной работе рассматривается случай, когда критерии равнозначимые и отсутствует возможность их ранжирования. Такие ситуации могут возникать, в частности, при разработке проектов для сложных экономических и технических объектов, оцениваемых с разных сторон. В качестве критериев могут выступать такие показатели, как стоимость проекта, время реализации, риски реализации, обеспеченность ресурсами и ряд других показателей. С точки зрения лиц, принимающих решение, мерой, определяющей отклонение выбираемого решения от оптимального, но недостижимого по набору критериев, могут служить потери по каждому показателю за счет достигнутого компромисса.
Цель исследования – разработка модели задачи многокритериальной оптимизации на основе учета потерь критериев в компромиссном решении.
Материалы и методы исследования
Основными материалами, использованными при подготовке данной статьи, явились монографии, статьи и электронные ресурсы, в которых рассмотрены вопросы многокритериальной оптимизации, теоретические обобщения и практические применения данных методов при решении практических задач. Методы проведения исследований основаны на использовании методов линейной алгебры, дискретной математики и теории множеств. В работе использованы алгоритмы численного моделирования для проверки работоспособности предлагаемых решений. Процедуры моделирования выполнены в программной среде Python с использованием прикладных пакетов оптимизации pulp, scipy.optimize, cvxopt.modeling. Для визуализации результатов работы алгоритмов оптимизации использован графический пакет matplotlib.
Результаты исследования и их обсуждение
Наиболее общим решением задачи многокритериальной оптимизации является нахождение множества Парето-оптимальных (эффективных) решений. Очевидно, что для любой предлагаемой модели решения задачи должны принадлежать этому множеству.
Обозначим множество допустимых решений задачи через X.
На множестве X рассмотрим задачу оптимизации с векторным критерием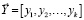 
. Введем на множестве X систему бинарных отношений:
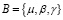, (1)
где μ – отношение эквивалентности; β – отношение несравнимости; γ – отношение предпочтения. Любые два решения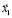 
и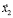 
из множества Х связаны одним из трех отношений таким образом, что
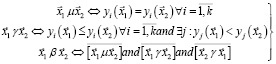. (2)
На основании введенных выше отношений (2) множество эффективных по Парето решений можно определить следующим образом:
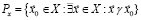. (3)
В работе [5] показано, что в случае выпуклости множества Х и выпуклости функций yi множество Px представляет собой связанное множество, что играет важную роль при построении алгоритмов нахождения эффективных решений. При этом множество Px может быть представлено конечной α-сетью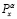 
эффективных решений:
,
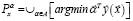где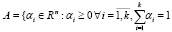
. (4)
В качестве примера рассмотрим двухкритериальную задачу линейного программирования, представленную следующими условиями:
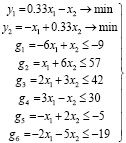. (5)
На рис. 1 представлена область допустимых решений задачи, точки A и B локальных экстремумов двух критериев. Множество эффективных решений для линейной задачи представляет собой отрезок AB, соединяющий две вершины многоугольника.
В общем случае для задач линейной оптимизации множество эффективных решений в n-мерном пространстве представляет собой выпуклый многогранник, размерность которого зависит в том числе от числа рассматриваемых в задаче критериев. Выделение множества эффективных решений в том или ином виде хотя и сужает область возможных решений многокритериальной задачи, однако неопределенность выбора итогового решения не устраняется.
Рассмотрим общую постановку задачи выбора решения многокритериальной задачи, основанную на понятии потерь по критериям при отклонении от их оптимума. Обозначим векторный критерий через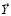 
, а вектор независимых переменных через 
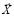. Будем считать, что функции векторного критерия 
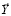определены на некотором допустимом множестве G.
Тогда задача определения оптимальных частных решений по каждому критерию может быть представлена в виде выражения
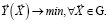(6)
Решения частных задач оптимизации образуют множество оптимальных решений, как подмножество Парето-оптимальных решений:
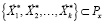. (7)
В общем случае решения векторной задачи (6) не совпадают, то есть
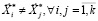. (8)
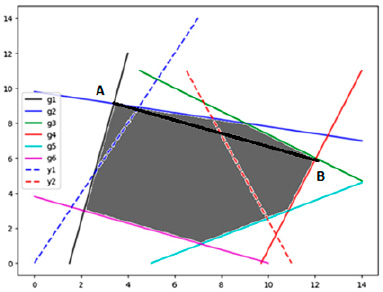
Рис. 1. Пример решения двухкритериальной задачи линейного программирования
Обозначим оптимальные решения по каждому критерию через vi. Тогда вектор решений можно записать в виде выражения
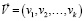. (9)
Пусть в качестве решения многокритериальной задачи выбран некоторый вектор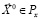 
, для которого значения по каждому из критериев можно записать в виде
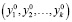. (10)
Образуем вектор потерь каждого критерия при выбранном решении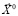 
как множество нормированных значений разниц оптимального и текущего значения критерия:
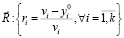. (11)
Использование понятия потерь критериев упрощает для лица, принимающего решение, оценку последствий выбора того или иного варианта решения, поскольку он может оперировать непосредственно показателями предметной области. В качестве решения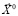 
многокритериальной задачи возможны несколько разных вариантов в зависимости от числа критериев и размерности множества G. Так, для двухкритериальной задачи в качестве решения может быть выбран вариант решения, соответствующий равенству потерь. Рассмотрим этот вариант решения на основе примера (5) для задачи линейного программирования с двумя критериями.
В таблице представлены результаты расчета эффективных по Парето решений на α-сети, а также значения критериев в узлах и потери критериев за счет отклонений от оптимальных значений.
Функции потерь критериев представлены на рис. 2.
Равенство потерь достигается на уровне 40 % от оптимальных по каждому критерию значений. В зависимости от предпочтений лица, принимающего решение, потери могут быть перераспределены. Данный алгоритм при выборе решения учитывает разную чувствительность критериев к изменению независимых переменных. Решение всегда смещается в факторном пространстве к оптимумам тех критериев, которые имеют большую чувствительность.
Рассмотрим использование данного подхода для нелинейной оптимизационной многокритериальной задачи. В качестве примера рассмотрим двухкритериальную задачу оптимизации состава портфеля ценных бумаг.
Точки α-сети эффективных решений
|
α |
x1 |
x2 |
y1 |
y2 |
r1 |
r2 |
|
0 |
12 |
6,0 |
-2,1 |
-10,0 |
0,7 |
0,0 |
|
0,1 |
11,1 |
6,3 |
-2,7 |
-9,0 |
0,7 |
0,1 |
|
0,2 |
10,2 |
6,6 |
-3,3 |
-8,0 |
0,6 |
0,2 |
|
0,3 |
9,3 |
6,9 |
-3,9 |
-7,0 |
0,5 |
0,3 |
|
0,4 |
8,4 |
7,2 |
-4,5 |
-6,0 |
0,4 |
0,4 |
|
0,5 |
7,5 |
7,5 |
-5,1 |
-5,0 |
0,4 |
0,5 |
|
0,6 |
6,6 |
7,8 |
-5,6 |
-4,0 |
0,3 |
0,6 |
|
0,7 |
5,7 |
8,1 |
-6,2 |
-3,0 |
0,2 |
0,7 |
|
0,8 |
4,8 |
8,4 |
-6,8 |
-2,0 |
0,1 |
0,8 |
|
0,9 |
3,9 |
8,7 |
-7,4 |
-1,0 |
0,1 |
0,9 |
|
1 |
3 |
9,0 |
-8,0 |
0,0 |
0,0 |
1,0 |
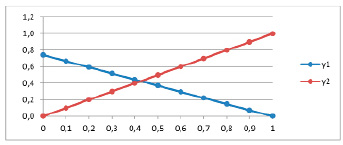
Рис. 2. Графики функций потерь на α-сети эффективных решений
Для множества активов А = {А1, А2, ... ,Аn} ожидаемая доходность может быть задана вектором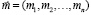 
, мера риска портфеля R задается вариацией V. Для расчета вариации будем использовать ковариационную матрицу
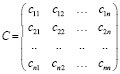. (12)
В качестве критериев будем рассматривать математическое ожидание доходности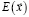 
и вариацию 
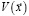, где:
, 
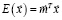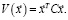(13)
Выполним моделирование задачи для пяти активов со следующими исходными данными:
,
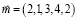. (14)
Задача оптимизации портфеля по Марковцу может быть записана следующим образом:
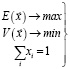. (15)
Обозначим экстремальные значения для критериев соответственно через E* и V*. На рис. 3 представлены построенные графики потерь по каждому критерию. Векторы оптимальных решений в данной задаче не совпадают, поэтому ищется компромиссное решение.
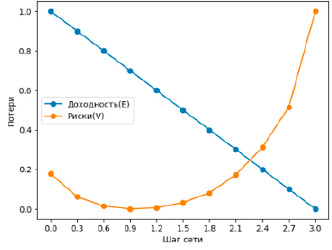
Рис. 3. Графики функций потерь
В случае отсутствия возможности назначить приоритет критериев логично в качестве решения выбрать вектор, обеспечивающий равные потери по каждому критерию.
В данном примере вектор решения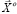 
= (0,12; 0,0; 0,32; 0,44; 0,12). Полученные решения определяют состав портфеля ценных бумаг. При этом равные потери по двум критериям составляют порядка 22 %.
Заключение
В данном исследовании рассматривается частный случай задач многокритериальной оптимизации, который отличается равной значимостью критериев и, как следствие, невозможностью их ранжирования. Для данного случая предлагается использовать подход, основанный на поиске решения при условии равенства потерь отдельных критериев. В работе рассматриваются примеры решения задач многокритериальной оптимизации для случая линейной векторной модели и модели с нелинейной целевой функцией. Алгоритм нахождения решения реализован с использованием библиотек оптимизации и средств визуализации программной среды Python. Предложенная модель многокритериальной оптимизации может найти применение при решении практических задач экономики и в проектной деятельности.