Подготовке студентов среднего профессионального образования (СПО) в настоящее время уделяется особое внимание, так как специалисты среднего звена востребованы в разных отраслях экономики: промышленности, сельском хозяйстве, строительстве, торговле, транспорте и связи, сфере слуг и др. Неслучайно в 2023 г. дан старт федеральному проекту «Профессионалитет», который призван усилить взаимодействие колледжа и отрасли, дать максимальную подготовку с максимальным трудоустройством.
В ссузах России (колледжах, техникумах, училищах), а также на факультетах среднего профессионального образования в вузах реализуется сегодня большое количество специальностей, которые готовят специалистов среднего звена для работы в различных сферах деятельности общества. Все специальности среднего профессионального образования объединены в группы. Для каждой группы специальностей разработаны федеральные государственные образовательные стандарты среднего профессионального образования (ФГОС СПО). Согласно этим стандартам, образовательная программа, реализуемая на базе основного общего образования, разрабатывается на основе требований федерального государственного образовательного стандарта среднего общего образования (ФГОС СОО) и федерального государственного образовательного стандарта среднего профессионального образования (ФГОС СПО) с учетом получаемой специальности.
Обучение математике в системе среднего профессионального образования реализуется на базовом и профильном уровнях (в зависимости от специальности), носит общеобразовательный характер и направлено на развитие логического, алгоритмического и математического мышления, формирование представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления. На профильном уровне математика, кроме этого, необходима для применения ее в специальных дисциплинах и для последующего обучения в вузе [1, с. 49].
Как показывает практика, в обучении математике студентов СПО возникает целый ряд проблем, основные из них следующие:
– низкое качество математической подготовки абитуриентов;
– отсутствие у большинства студентов первого курса сформированных общеучебных умений, навыков организации самостоятельной работы, мыслительной деятельности; недостаточная развитость коммуникативных умений;
– большой объем учебного материала (двухгодичный курс математики средней школы должен быть пройден за один год) и изучение его большими блоками;
– недостаточность научно-методических рекомендаций по внедрению современных образовательных технологий в процесс обучения математике;
– отсутствие достаточного количества учебников математики для СПО, иногда обучение математике ведется по учебникам для средней школы и т.д.
Одним из путей выхода из создавшейся ситуации является вовлечение студентов в активный процесс получения знаний с привлечением приемов эвристической деятельности.
Цель исследования – спроектировать и описать методические приемы организации эвристической деятельности студентов СПО в процессе решения ими математических задач.
Материалы и методы исследования
Использовались федеральные государственные образовательные стандарты среднего общего образования и среднего профессионального образования, относящиеся к группе специальностей 44.00.00 Образование и педагогические науки. Проводился анализ научно-методической литературы и рабочих программ по математике для специальностей, изучающих математику на базовом и профильном уровнях, а также анализ учебников математики, специально созданных для СПО и применяемых на практике, с целью выявления возможностей формирования у студентов приемов эвристической деятельности. Из экспериментальных методов применялись: беседы с преподавателями СПО, наблюдение за процессом решения задач, анкетирование студентов.
Результаты исследования и их обсуждение
Исследуя особенности обучения математике в системе среднего профессионального образования и возникающие при этом проблемы, было установлено, что изучение этой дисциплины должно быть направлено, прежде всего, на формирование общеучебных компетенций, к которым относятся умения и способы самоорганизации, самообучения, а также информационные и коммуникативные компетенции. На основе общеучебных компетенций должны формироваться общие компетенции, зафиксированные в стандарте СПО.
Для эффективной организации учебной и самостоятельной деятельности обучающихся по программам СПО большое значение имеет выбор приемов и методов обучения. Одной из основных задач среднего общего образования на современном этапе является развитие творческого потенциала учащихся, а также создание условий для их саморазвития и самореализации. Поэтому наряду с традиционными методами в структуру занятий со студентами СПО необходимо включать и присущие активным методам обучения компоненты. Одним из активных методов обучения математике является эвристический метод и составляющие его приемы эвристической деятельности, позволяющие вовлечь каждого студента в активный процесс получения знаний. Овладение этими приемами есть неотъемлемый признак развития у обучающихся творческого нестандартного мышления.
В энциклопедическом словаре термин «эвристика» трактуется в разных смыслах: 1) специальные методы, используемые в процессе открытия нового (эвристические методы); 2) наука, изучающая продуктивное творческое мышление (эвристическая деятельность); 3) восходящий к Сократу метод обучения (так называемые сократические беседы).
В методике обучения математике под эвристикой понимают всякий способ, применение которого может привести к отысканию метода решения задачи или доказательства теоремы.
Вопросы организации эвристической деятельности на уроках математики, использования эвристических методов обучения, формирования у учащихся эвристических приемов рассматривали в своих работах В.И. Андреев, В.Н. Введенский, В.А. Далингер, Т.С. Жукова, И.И. Ильясов, М.М. Левина, О.К. Огурцова, Д. Пойа, Г.И. Саранцев, Е.И. Скафа, Е.Е. Семенов, А.В. Хуторской и др. В частности, Е.И. Скафа разработала теоретико-методические основы формирования приемов эвристической деятельности учащихся при обучении математике в условиях внедрения современных технологий обучения [2, с. 272].
Под учебно-познавательной эвристической деятельностью сегодня понимается деятельность обучающихся, организованная и управляемая учителем с использованием разнообразных эвристических приемов, методов и средств, направленная на создание новой системы действий по поиску неизвестных ранее закономерностей, на формирование процессов, обеспечивающих познавательную и творческую деятельность, в результате которой учащиеся активно овладевают знаниями, развивают эвристические умения и личностные качества [3; 4].
Эвристические приемы рассматривают как особые приемы, составляющие поисковые стратегии и тактики, определяющие самое общее направление мысли, сформированные в ходе решения одних задач и более или менее сознательно переносящиеся на другие задачи [3, 5].
В работах Г.И. Саранцева, Т.С. Жуковой, И.В. Ульяновой и др. обоснована роль математических задач в обучении учащихся эвристикам. Авторы на геометрическом материале выделяют базовые эвристики и специальные эвристики. Основой базовых эвристик являются действия выведения следствий, преобразования требования задачи в равносильное ему, составления промежуточных задач и т.д. Специальные эвристики обусловлены содержанием учебного материала. Введение, усвоение и применение таких эвристик осуществляется в процессе развития этого материала [5–7].
Анализу эвристических приемов решения задач и конструированию их системы посвящена монография И.И. Ильясова [8, с. 49]. Практические рекомендации по организации поисковой-исследовательской деятельности учащихся при обучении математике представлены в работах В.А. Далингера, Л.С. Капкаевой [9; 10]. Педагогический потенциал эвристического обучения раскрыт в работе Г.М. Щевелевой и В.Ф. Манухова. Авторы рассматривают основные идеи, закономерности и методики эвристической деятельности при подготовке студентов различных профилей на разных уровнях обучения [11, с. 129].
В дальнейшем под приемами эвристической деятельности будем понимать приемы, основанные на специальных эвристиках, которые помогают формировать не только знания, но также умения и потребности применять эти знания для анализа, оценки ситуации и принятия правильного решения. Такие умения особенно необходимы специалисту среднего звена в своей профессиональной деятельности.
Так как основным видом деятельности студентов СПО в обучении математике является решение задач, то формирование эвристических приемов и эвристического мышления должно происходить в процессе освоения методов решения задач разных типов. Использование приемов эвристической деятельности при этом позволит обучающимся самостоятельно осуществлять поиск решения задач различной сложности, в том числе и нестандартных, делать свои собственные «открытия», самостоятельно находить выход из проблемных ситуаций.
Из всех разделов математики, изучаемых студентами СПО, большим творческим потенциалом обладает раздел, посвященный началам математического анализа. Кроме того, он открывает широкие возможности для иллюстраций применимости математики к решению прикладных задач. Большое влияние данный раздел оказывает и на формирование мировоззрения обучающихся. Владение методами дифференциального и интегрального исчислений позволяет на содержательных примерах изучать различные процессы, показать универсальность математических методов и т.д. Знания, умения и способы деятельности, приобретаемые студентами при изучении производной, интеграла и их приложений, особенно активно применяются в геометрии, физике и информатике. Отсюда следует значимость неформального усвоения базовых понятий и методов математического анализа, и большую роль в этом играет эвристическая деятельность.
Так, при изучении разделов «Производная и ее геометрический смысл», «Применение производной к исследованию функций» решаются следующие основные типы задач:
1) на нахождение угла между касательной к графику функции в точке x0 и осью Ox;
2) на нахождение угла между осью Oy и касательной к графику функции в данной точке;
3) на нахождение угла, под которым пересекаются графики функций;
4) на нахождение точек графика функции, в которых касательная к этому графику параллельна (перпендикулярна) данной прямой;
5) на нахождение точек экстремума или самого экстремума функции;
6) текстовые задачи на нахождение наибольшего и наименьшего значений функции.
Решение задач первого типа на нахождение угла между касательной к графику функции в данной точке и осью Ox начинается с обсуждения следующих вопросов:
– Как связан искомый угол с производной функции в точке? (Тангенс этого угла равен производной функции в точке.)
– Как найти производную данной функции? (Надо сначала записать функцию в виде, удобном для применения правил дифференцирования.)
– Как найти значение производной функции в точке x0? (Подставить x0 в выражение производной функции.)
– Что выражает собой значение производной функции в точке x0? (Тангенс угла между касательной к графику функции в точке x0 и осью Ox. Зная тангенс, можно найти сам угол.)
Таким образом, в ходе решения задач этого типа студенты знакомятся с эвристикой:
А) Чтобы найти угол между касательной к графику функции в точке x0 и осью Ox, надо найти значение производной данной функции в этой точке, оно равно тангенсу искомого угла.
Эта эвристика применяется затем при решении задач второго типа на нахождение угла между осью Oy и касательной к графику функции в данной точке.
В ходе решения со студентами обсуждаются следующие вопросы:
– Как связаны угол, между касательной к графику функции в точке и осью Ox и угол между этой касательной и осью Oy? (Возможны разные случаи: если угол между касательной и осью Ox острый, то сумма этих углов равна π/2; если этот угол тупой, то угол между касательной и осью Oy равен разности градусной меры этого угла и π/2.)
– Можно ли найти угол, образованный касательной к графику функции и осью Ox? (Да, можно, так как тангенс этого угла есть значение производной функции в данной точке.)
– Как найти искомый угол, если известен угол между касательной к графику функции в точке и осью Ox? (Надо от π/2 отнять градусную меру этого угла.)
В результате такой эвристической деятельности студенты формулируют правило:
Б) Чтобы найти угол между осью Oy и касательной к графику функции в данной точке, надо найти сначала угол между этой касательной и осью Ox (пусть это угол α), затем:
1) если угол α острый, то от π/2 отнять градусную меру угла α;
2) если угол α тупой, то от градусной меры этого угла отнять π/2.
Решение задач третьего типа на нахождение угла, под которым пересекаются графики функций, приводит студентов к новой эвристике. Сначала в ходе эвристической беседы обсуждаются вопросы типа:
– Что называется углом между кривыми в точке их пересечения? (Углом между двумя кривыми называется угол между их касательными.)
– Как найти точку пересечения графиков функций? (Надо приравнять правые части функций и решить полученное уравнение.)
– Можно ли сразу найти угол, под которым пересекаются кривые? (Нет, нельзя.)
(Большую роль в поиске решения здесь играет чертеж. Рассмотрим случай графической модели задачи, представленной на рис. 1.)
– Какие углы можно найти? (Углы, которые образуют касательные к графикам данных функций с положительным направлением оси Ox.)
– Как найти угол, который образует первая касательная с положительным направлением оси Ox? (Надо найти значение производной первой функции в точке пересечения графиков, это будет тангенс первого угла, по тангенсу найти угол, например α.)
– Как найти угол, который образует вторая касательная с положительным направлением оси Ox? (Надо найти значение производной второй функции в точке пересечения графиков, это будет тангенс второго угла, по тангенсу найти угол, например β.)
– Как найти искомый угол между двумя кривыми? (Надо найти разность α – β.)
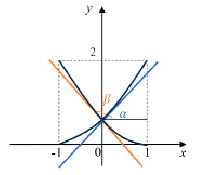
Рис. 1. Графическая модель задачи третьего типа
После обсуждения этих вопросов и решения конкретных задач данного типа студентами формулируется эвристика:
В) Чтобы найти угол между двумя кривыми, следует найти угол между их касательными в точке пересечения кривых, для этого надо найти с помощью производной два угла, которые образуют касательные с положительным направлением оси Ox, затем найти разность их градусных мер.
Таким образом, в процессе решения задач первых трех типов у обучающихся формируются действия, составляющие первый прием эвристической деятельности:
I. Прием, основанный на применении геометрического смысла производной. Он состоит из эвристик А), Б), В), которые помогают найти: угол между касательной и осью Ox; угол между касательной и осью Oy; угол между двумя кривыми.
При решении задач четвертого типа на нахождение точек графика функции, в которых касательная к этому графику параллельна (перпендикулярна) данной прямой, происходит формирование эвристик, составляющих прием, основанный на применении уравнения касательной.
Решение задач этого типа начинается с обсуждения вопросов:
– Какой вид имеет уравнение касательной к графику функции y = f(x) в точке x0? (Уравнение касательной имеет вид
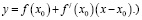
– При каком условии две прямые, заданные уравнениями с угловыми коэффициентам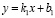и 
и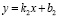 
, параллельны? (Когда у них угловые коэффициенты равны.)
– Чему равен коэффициент при x в уравнении касательной? (Значению производной данной функции в точке.)
– Как найти производную функции, данной в задаче? (По правилам нахождения производной; если функция сложная, то сначала найти производную «внешней» функции и умножить на производную «внутренней» функции.)
– Как теперь найти искомые точки графика данной функции? (Надо производную функции приравнять к угловому коэффициенту прямой и решить полученное уравнение, так найдем абсциссы точек касания, а затем и ординаты.)
Итак, в ходе эвристической беседы и решения конкретных задач данного типа студенты знакомятся с новым эвристическим приемом.
II. Прием, основанный на применении уравнения касательной к графику функции в данной точке. Он состоит из двух эвристик:
А) Чтобы найти точки, в которых касательная к графику функции параллельна прямой y = kx, надо записать уравнение касательной в общем виде и приравнять коэффициенты при x в уравнении касательной и уравнении прямой, затем решить уравнение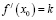 
.
Б) Чтобы найти точки, в которых касательная к графику функции перпендикулярна прямой y = kx, надо записать уравнение касательной в общем виде и приравнять коэффициент при x в уравнении касательной к выражению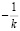 
, т.е. решить 
.
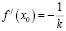Большую роль в обучении математике и математическом развитии студентов СПО играют задачи на нахождение точек экстремума и самого экстремума заданной функции. Задачи такого типа имеют практико-ориентированную направленность, в своей профессиональной деятельности специалистам среднего звена часто приходится сталкиваться с необходимостью принять наилучшее возможное (т.е. оптимальное) решение. Огромное число подобных проблем возникает в экономике, технике, транспорте и других сферах деятельности человека. Рассмотрим прием эвристической деятельности, используемый при решении таких задач.
III. Прием, основанный на использовании производной для нахождения точек экстремума функции. Он включает следующие действия:
Чтобы найти точки экстремума (максимума и минимума) функции, надо:
1) найти производную данной функции;
2) приравнять производную к нулю и решить полученное уравнение, так найдем стационарные точки функции;
3) установить, меняется ли знак производной при переходе через каждую стационарную точку функции, если знак меняется с плюса на минус, то это точка максимума, а если с минуса на плюс, то это точка минимума. Проиллюстрируем на примере применение этого приема.
Пример 1. Найти точки экстремума функции
.
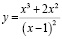Решение начинается с эвристической беседы:
– Что такое точки экстремума? (Это точки максимума и минимума.)
– Какими особенностями обладают точки экстремума? (Производная в них равна 0.)
– Как найти производную данной функции? (Производную найдем по правилу производной частного.)
– Все ли точки, в которых производная равна нулю, являются точками экстремума? (Нет, не все, а лишь те точки, при переходе которых производная меняет знак.)
– Какие точки, в которых производная равна нулю, будут точками максимума, а какие – точками минимума? (Если при переходе через точку производная меняет знак с плюса на минус, то это точка максимума, а если с минуса на плюс, то точка минимума.)
После такой беседы выполняется решение задачи.
При решении задач других типов, организуя эвристическую деятельность, можно выделить вместе со студентами другие приемы и составляющие их действия.
IV. Прием, основанный на правилах вычисления первообразной и интеграла. Он применяется при вычислении интегралов функций и опирается на следующие эвристики:
Чтобы вычислить интеграл от заданной функции, надо:
1) установить, что представляет собой функция (сумму, разность, произведение, частное), к какому типу функций она относится (степенной, показательной, тригонометрическим и т.д.);
2) выяснить, можно ли преобразовать функцию к виду, удобному для интегрирования;
3) найти первообразную функции, используя правила и таблицу первообразных;
4) вычислить значение первообразной в верхнем и нижнем пределах интегрирования и найти их разность.
Эвристики особенно необходимы при решении задач на вычисление площадей фигур с помощью интеграла. Рассмотрим их подробнее.
V. Прием, основанный на применении интеграла к вычислению площадей фигур.
А) Чтобы найти площадь фигуры, ограниченной сверху графиком функции y = f(x), снизу отрезком [a,b] оси Ox и с боков прямыми x = a и x = b, надо применить формулу для вычисления площади криволинейной трапеции
.
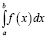Б) Чтобы найти площадь фигуры, ограниченной сверху графиком функции y = f(x), а снизу графиком функции y = g(x) (рис. 2), надо вычислить интеграл от функции, равной разности между «верхней» и «нижней» функциями, т.е.
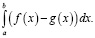
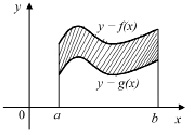
Рис. 2. Фигура, ограниченная сверху и снизу графиками функций
В) Чтобы найти площадь фигуры, ограниченной сверху графиками двух функций y = f(x) и y = g(x), снизу осью Ox, с боков прямыми x = a и x = b (рис. 3), надо разбить эту фигуру на две криволинейные трапеции, вычислить их площади и результаты сложить.
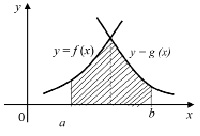
Рис. 3. Фигура, ограниченная сверху графиками двух функций
Г) Чтобы найти площадь фигуры, ограниченной снизу графиком функции, принимающей отрицательные значения, а сверху отрезком [a,b] оси Ox (рис. 4), следует применить формулу для вычисления площади криволинейной трапеции со знаком «минус».
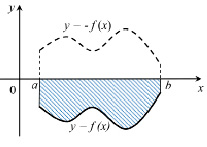
Рис. 4. Фигура, ограниченная снизу графиком функции, а сверху – осью Ox
Д) Чтобы найти площадь фигуры, ограниченной сверху графиком функции y = c (c – константа), а снизу – графиком функции y = f(x) и осью Oy, надо сначала найти площадь прямоугольника, а затем из нее вычесть площадь подграфика функции y = f(x).
Проиллюстрируем использование некоторых эвристик на примере.
Пример 2. Найти площадь фигуры, ограниченной прямой y = 1, осью Oy и графиком функции y = sin x при 0 ≤ x ≤ π/2.
Решение этой задачи начинается с построения чертежа (рис. 5) и эвристической беседы:
– Какими линиями ограничена фигура? (Сверху прямой y = 1, слева осью Oy, снизу графиком функции y = sin x.)
– Является ли полученная фигура криволинейной трапецией? (Нет, так как она ограничена снизу не осью Ox, а графиком функции y = sin x.)
– Как можно найти площадь этой фигуры? (Ответы могут быть разные: 1) вычислить сразу площадь фигуры, ограниченной сверху и снизу графиками функций y = 1 и y = sin x по соответствующей формуле; 2) найти сначала площадь прямоугольника, ограниченного линиями: y = 1, x = 0, x = π/2, y = 0, а затем из нее вычесть площадь криволинейной трапеции, ограниченной сверху синусоидой; 3) рассматривать данную фигуру как криволинейную трапецию, примыкающую к оси Oy, но с таким вариантом студенты, возможно, незнакомы, и он может вызвать у них затруднение.)
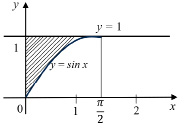
Рис. 5. Графическая модель к задаче 2
Можно всех учащихся разделить на группы и решить эту задачу разными способами.
VI. Прием, основанный на применении правила нахождения наибольшего (наименьшего) значения функции на заданном промежутке.
Большое значение для студентов всех специальностей СПО имеет умение строить математические модели реальных ситуаций, явлений, процессов и т.д., которое формируется в основном при решении текстовых задач. Эти задачи не имеют какого-либо алгоритма решения, поэтому здесь особенно необходима организация эвристической деятельности обучающихся. Специальные эвристики в данном случае направляют ход решения текстовой задачи, ведут к получению результата рациональным путем. При изучении производной и ее приложений решаются текстовые задачи на нахождение наименьшего и наибольшего значений. Они играют особую роль в обучении студентов СПО, так как учат находить оптимальное решение в заданной ситуации. Набор таких задач и методика формирования некоторых приемов их решения приведены в наших работах [12; 13].
Приведем перечень эвристических вопросов, направляющих поиск решения задач данного типа и определяющих действия, составляющие названный прием.
1) О наименьшем (наибольшем) значении какой величины говорится в задаче? (Необходимо из текста задачи выявить величину, о наименьшем (наибольшем) значении которой говорится в задаче.)
2) Какой формулой выражается значение данной величины? (Необходимо записать формулу для величины, о наименьшем (наибольшем) значении которой говорится в задаче.)
В условии практико-ориентированных задач такого типа бывает дана еще одна известная величина, поэтому необходимо ответить на следующий вопрос:
3) Какой формулой выражается значение известной в задаче величины? (Следует записать эту формулу.)
4) Какую из двух неизвестных величин в формуле искомой величины удобно принять за независимую переменную? (Одну из неизвестных в формуле величин следует принять за независимую переменную x и указать интервал ее изменения.)
5) Как выразить вторую неизвестную величину в формуле через x? (Надо использовать известные в задаче величины.)
6) Как выразить теперь величину, о наименьшем (наибольшем) значении которой говорится в задаче, как функцию введенной переменной x? (Надо подставить в ее формулу выражения неизвестных величин через x.)
7) Как найти наименьшее (наибольшее) значение составленной функции на заданном интервале? (Надо найти производную этой функции, ее стационарные точки, принадлежащие заданному интервалу; если такая точка одна, то надо исследовать ее на экстремум: если это точка минимума, то функция принимает в ней наименьшее значение, а если точка максимума, то наибольшее значение.)
8) Как найти то, что требуется в задаче? (Иногда в задачах такого типа требуется найти не саму функцию, о наименьшем (наибольшем) значении которой говорится в задаче, а ее составляющие величины, в этом случае надо найти их по составленным выражениям и введенной переменной x.)
Проиллюстрируем организацию эвристической деятельности на конкретном примере.
Пример 3. Определить размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Решение задачи начинается с построения чертежа, эвристической беседы и одновременно выполнения действий, ведущих к получению необходимого результата.
– Какую форму имеет бассейн? (Форму прямоугольного параллелепипеда с квадратным основанием без верха.)
– О наименьшем значении какой величины говорится в задаче? (О наименьшем значении площади поверхности прямоугольного параллелепипеда без верхней грани.)
– Чему равен объем прямоугольного параллелепипеда? (Так как у бассейна квадратное дно, то его объем равен: V = a2h, гда а – сторона основания, h – высота.)
– Чему равна площадь поверхности бассейна? (Sп = 4ah + a2)
– Какую из двух неизвестных величин а и h удобно принять за независимую переменную x? (Пусть a = x, x > 0)
– Как выразить вторую неизвестную величину через x и известную в задаче величину? (Надо использовать формулу для объема: V = x2h, так как V = 32, то h = 32/x2.)
– Как теперь выразить площадь поверхности через x? (Надо подставить в формулу площади выражения а и h через x, тогда получим:
Sп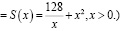 
– Как найти наименьшее значение функции S(x) на заданном интервале x > 0? (Надо найти производную этой функции, затем ее стационарные точки, принадлежащие указанному интервалу, если точка одна, то надо исследовать ее на экстремум.)
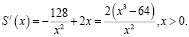
Решая уравнение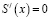 
, получим x = 4 – стационарная точка, принадлежащая данному интервалу. Исследование приводит к тому, что x = 4 является точкой минимума. Следовательно, функция S(x) принимает в ней наименьшее значение
– Как ответить на вопрос задачи? (Размеры открытого бассейна: a = 4, h = 2). Заключение
Обучение математике студентов по программе среднего профессионального образования имеет свои особенности, связанные как с содержанием учебного предмета «Математика», которое должно быть освоено за один год вместо двух лет в средней школе, методами и формами обучения, так и низким уровнем математической подготовки поступающих, несформированностью общеучебных умений и т.д. Поэтому для достижения целей обучения математике в среднем профессиональном образовании необходимо наряду с традиционными методами использовать активные методы обучения, в частности приемы эвристической деятельности. Основанные на специальных эвристиках эти приемы помогают формировать не только знания, но и умения применять эти знания для анализа, оценки ситуации и принятия правильного решения. Такие умения особенно необходимы специалисту-практику.
Приведенные выше примеры организации эвристической деятельности студентов СПО в процессе решения задач наглядно демонстрируют логическую схему рассуждений студента при поиске решения задачи и алгоритмичность его действий. Выявленные приемы и составляющие их эвристики студенты могут использовать в дальнейшем для самостоятельного решения задач, приобретая при этом опыт творческой деятельности.