Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Создание современных сложных технических объектов (в частности, современных энергосистем) невозможно без новых математических моделей и вычислительных методов решения широкого спектра задач, связанных с эффективным моделированием и изучением динамики функционирования технических объектов и систем. Это требует построения математической модели, адекватно описывающей физический объект, и идентификации параметров и функций, входящих в эту модель. Многие задачи моделирования и управления реальных объектов приводят к необходимости использования интегральных уравнений Вольтерра I рода, связывающих выходной и входной сигналы исследуемой системы и играющих существенную роль в задачах математического моделирования динамических систем во временной области. К настоящему времени этому классу математических моделей посвящено большое количество статей и монографий. Обширный обзор современных исследований в этом направлении приведен в монографии [1, р. 36].

Для линейных стационарных систем достаточно распространенной моделью типа «вход – выход» в условиях отсутствия априорной информации о структуре физическом устройстве является интегральное уравнение Вольтерра I рода [2, 3]:

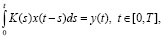(1)

в котором t – время, x(t) – входной сигнал, y(t) – выходной сигнал, K(s) – ядро Вольтерра (или другими словами – импульсная переходная функция системы). Задача оценивания ядра K(s) уравнения (1) (или импульсной переходной функции – термин теории систем автоматического управления) по заданным сигналам x(t), y(t) получила название непараметрической идентификации.

Если параметры системы меняются в процессе эксплуатации системы, то такие системы получили название нестационарных систем, и для них в качестве математической модели «вход – выход» используют интегральное уравнение Вольтерра вида

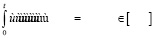(2)

где ядро Вольтерра K(t,s) есть уже функция двух аргументов s, t, таких, что 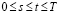. В силу универсальности уравнение (2) хорошо зарекомендовало себя в задачах моделирования различных технических объектов [2, 4, 5]. Эта же интегральная математическая модель используется для моделирования полета различных летательных аппаратов [6, c. 17]. Следует отметить, что идентификация импульсной переходной функции K(t,s) позволяет оценить изменяющиеся во времени коэффициенты обыкновенного дифференциального n-го порядка, которое описывает поведение выходного сигнала y(t) нестационарной системы [2], т.е. получить дифференциальную модель для описания динамики исследуемого процесса. Все это говорит о том, что интегральная модель (2) широко используется для моделирования динамических объектов в различных областях науки и техники, а задача оценивания импульсной переходной функции K(t,s) с приемлемой для практики точностью по экспериментальным данным, отягощенным случайными погрешностями измерения, является актуальной задачей математического моделирования нестационарных динамических систем.

В общем случае идентификация функции K(t,s), так же как и идентификация ядра в (1), является некорректно поставленной задачей [7, с. 18]. В таких задачах решение задачи может не существовать, может быть не единственным и решение может быть неустойчиво к погрешностям задания исходных данных (в задаче идентификации исходными являются значения входного и выходного сигналов идентифицируемой системы). Заметим, что для решения таких некорректных задач используют специальные методы – методы регуляризации [7, с. 53]. Как правило, уравнение (2) аппроксимируется системой линейных алгебраических уравнений (вырожденной или плохо обусловленной), для устойчивого решения которой используют регуляризирующие алгоритмы [7, c. 114]. Такой подход в случае рассматриваемой задачи непараметрической идентификации имеет ряд существенных недостатков: вызывает большие систематические ошибки получаемого решения из-за ошибок аппроксимации исходного уравнения Вольтерра; обуславливает трудности с учетом и компенсацией погрешностей измерения входного сигнала; выбором параметра регуляризации.

Цель данной работы – изложить новый способ непараметрической идентификации двумерного ядра уравнения Вольтерра с использованием входных сигналов из класса кусочно-линейных функций, а также разработать устойчивый к шумам измерений вычислительный алгоритм идентификации.

Объектом исследования являются нестационарные линейные системы, математической моделью которых является интегральное уравнение Вольтерра I рода вида (2).

Актуальность и значимость данной работы обусловлена следующими моментами:

− разработанный на основе предлагаемого подхода алгоритм идентификации двумерного ядра Вольтерра K(t,s) имеет низкую методическую ошибку за счет хорошей точности аппроксимации входного и выходного сигналов идентифицируемой системы кубическими сплайнами;

− использование сглаживающих кубических сплайнов позволяет (при соответствующем выборе параметра сглаживания кубического сплайна) учесть и существенно уменьшить влияние погрешностей регистрации сигналов идентифицируемой системы, что приводит к значительному уменьшению общей ошибки идентификации по сравнению с другими известными алгоритмами идентификации;

− алгоритм идентификации обладает достаточной универсальностью, единственным значимым ограничением которого является активная форма процедуры идентификации с генерацией кусочно-линейного входного сигнала;

− предлагаемый в статье алгоритм идентификации может быть успешно применен при решении задач непараметрической идентификации более сложных технических систем, например идентификации систем с векторным входом, к которым относятся некоторые объекты теплоэнергетики [8].

Материалы и методы исследования

Как уже отмечалось, в качестве математической модели линейных стационарных систем в условиях отсутствия априорной информации о структуре физическом устройстве выступает интегральное уравнение Вольтерра I рода вида (1). В теории автоматического управления хорошо известен подход к идентификации ядра K(s), основанный на применении кусочно-постоянного входного сигнала в виде функции Хевисайда, определяемой соотношением

Обозначим через ye(t) выходной сигнал системы при входе e(t), при допущениях, что ye(0) = 0 и первая производная y'e(t) непрерывна на интервале [0, T], имеет место равенство 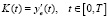. Это означает, что для оценивания ядра K(t) достаточно вычислить (с приемлемой ошибкой) первую производную выходного сигнала ye(t). Возникает вопрос: можно ли получить аналогичную формулу обращения для непараметрической идентификации нестационарных линейных систем (2). Ответ положителен, но при использовании в качестве входного воздействия на идентифицируемую систему специального сигнала – кусочно-линейного сигнала. Кратко изложим получение такой формулы.

Пусть модель (2) описывает динамику линейной нестационарной системы со скалярным входом x(t) и скалярным выходом y(t), таким что y(0) = 0. Обозначим через CΔ пространство функций, непрерывных на заданном интервале Δ изменения аргумента функций. Развивая методику, разработанную в [9, 10], рассмотрим специфику идентификации функции K(t,s) в (2) с помощью однопараметрического семейства входных сигналов, определяемого выражением

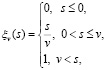(3)

где параметр v > 0 соответствует времени нарастания фронта тестового сигнала. Заметим, что такие входные сигналы могут быть достаточно просто реализованы в активном эксперименте идентификации различных технических устройств. Тогда исходная задача идентификации K(t,s) редуцируется к решению уравнения Вольтерра I рода

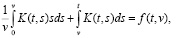(4)

,

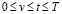в котором f(t,v) – отклик динамической системы на вход вида (3). Пусть

,

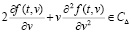f(0, 0) = 0, .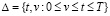

Тогда решение K(t,v) в классе непрерывных на Δ функций может быть найдено в явном виде [9]:

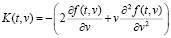. (5)

Как видно из формулы (5), для нахождения ядра K(t,v) требуется вычислить частные производные первого и второго порядка функции f(t,v) по переменной v. Однако при численной реализации этой формулы возникают трудности, обусловленные следующими причинами:

− значения функции f(t,v) регистрируются на дискретных множествах точек

;

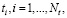
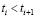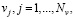
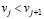; (6)

− зарегистрированные в этих точках значения функции f(ti,vj) содержат случайные погрешности ηi,j и допускают представление

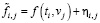; (7)

− вычисление производных является некорректно поставленной задачей [7, с. 18], когда незначительные погрешности задания дифференцируемой функции могут привести к значительным ошибкам в производных, что в конечном итоге вызовет большие ошибки решения (8).

Для преодоления этих трудностей будем использовать методы сплайн-функций [11, с. 96], а конкретнее – сглаживающие кубические сплайны (СКС), широко используемые при обработке экспериментальных данных [12, с. 34]. Кратко приведем некоторые определения СКС, необходимые для дальнейшего построения устойчивого алгоритма идентификации (для подробного изучения СКС рекомендуем обратиться к работам [11, с. 96; 12, с. 64]).

Предположим, что на некотором интервале [V1,V2] заданы Nv узлов 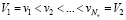, и в этих узлах измерены значения некоторого сигнала g(v)

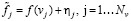, (8)

где ηj – случайный шум измерений с нулевым средним и дисперсией 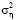(равноточные измерения). Функция 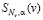называется сглаживающим кубическим сплайном (СКС) дефекта единица, если:

− на каждом отрезке 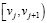функция 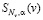является кубическим многочленом вида

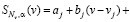
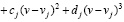; (9)

− функция 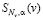дважды непрерывно дифференцируема на всем интервале [V1,V2];

− в общем случае СКС не проходит через точки 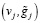, а проходит более «плавно» в некоторой окрестности этих точек (зависящей от величины параметра сглаживания α, меняющегося в пределах 0<α<∞), обеспечивая тем самым сглаживание (фильтрацию) шума измерений.

Для однозначного вычисления коэффициентов сплайна aj, bj, cj, dj в (9) (зависящих от параметра сглаживания) задают краевые условия в узлах v1, 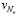. Наиболее часто используются следующие условия [11, с. 97]:

− условия на вторые производные сплайна (естественные краевые условия):

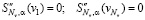; (10)

− условия на первые производные сплайна:

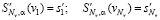, (11)

а также комбинация этих условий (например, слева – условие (11), справа – (10)).

Для вычисления коэффициентов сплайна (при заданном параметре сглаживания) составляется система линейных алгебраических уравнений c пятидиагональной матрицей относительно некоторого вектора (как правило, это значения второй производной сплайна в узлах {vj}), через проекции которого затем находятся все коэффициенты представления (9) СКС. Вычислительные алгоритмы нахождения коэффициентов СКС подробно изложены в [11, с. 151–154; 12, с. 44–49] и здесь не приводятся.

Параметр сглаживания α «управляет» гладкостью сплайна, и ошибка сглаживания (как и ошибка дифференцирования) существенно зависит от величины этого параметра. Заметим, что при α = 0 СКС становится интерполяционным сплайном (проходит через точки 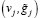), при α = ∞ СКС становится прямой линией. Между двумя этими предельными значениями существует значение параметра (назовем его оптимальным), для которого ошибка сглаживания (в принятой норме) минимальна. Временно предположим, что приемлемое (с точки зрения минимума ошибки сглаживания) значение параметра сглаживания может быть найдено (выбор рассматривается в следующем разделе).

Тогда предлагаемый алгоритм идентификации можно представить следующими шагами:

Шаг 1. Для каждого значения i = 1,…,Nt формируются исходные (для построения сглаживающего сплайна) данные

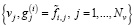(12)

и задаются краевые условия, комбинация которых определяется исходя из имеющейся априорной информации о функции f(t,v) в крайних точках интервала [V1,V2] (при отсутствии такой достоверной информации следует обратиться к естественным условиям (10)).

Шаг 2. Выбирается параметр сглаживания α1(i), и по исходным данным (12) строится СКС 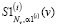, по которому затем вычисляется первая производная 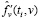(оценка производной ).

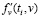Шаг 3. Для каждого значения i = 1,…,Nt формируются исходные данные

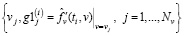(13)

и задаются соответствующие краевые условия в крайних точках интервала [V1,V2].

Шаг 4. Выбирается параметр сглаживания α2(i), и по исходным данным (13) строится СКС 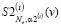, первая производная которого является оценкой 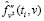для второй производной .

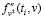Шаг 5. Вычисленные производные 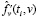, 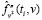подставляются в формулу (5) и находятся значения оценки 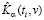на дискретном множестве точек .

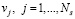Таким образом, шаги 2–5 повторяются для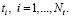

Так как построение СКС при заданном параметре сглаживания требует примерно Copen ∙ Nv, где Copen ≈ 30, арифметических операций [11, с. 345], то предлагаемый алгоритм идентификации имеет высокую вычислительную эффективность даже при большой размерности сетки (ti, vj). Однако остается открытым вопрос о выборе параметра сглаживания СКС.

Выбор параметра сглаживания при неизвестной дисперсии шума

При построении и использовании алгоритмов выбора параметра сглаживания при решении задач идентификации следует выделить две ситуации:

− дисперсия 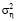шума измерений известна (с точностью 5–10 %);

− дисперсия шума неизвестна (это наиболее часто встречается при идентификации с использованием реальных экспериментальных данных).

В первом случае можно обратиться к алгоритмам, которые существенно используют дисперсию шума. Их анализ [12, с. 60–67] показал, что алгоритм выбора, построенный на основе проверки критерия оптимальности линейного алгоритма фильтрации, позволяет с приемлемой точностью (5–8 %) оценить значения оптимального параметра сглаживания, минимизирующего величину среднеквадратической ошибки сглаживания. Однако если дисперсия шума известна с большой ошибкой, то это вызовет существенное отличие (в несколько раз и более) оценки от оптимального параметра сглаживания.

Очевидно, что ситуация, когда дисперсия шума неизвестна с требуемой точностью, наиболее характерно при решении практических задач идентификации. Для нахождения приемлемого значения параметра сглаживания в этом случая обратимся к методу L-кривой, который рассматривается в зарубежных публикациях, например [13, 14], для выбора параметра регуляризации в алгоритмах решения линейных некорректных задач. В работе [15] была сделана следующая модификация метода L-кривой для выбора параметра сглаживания. Приведем конечные соотношения алгоритма выбора параметра сглаживания (подробно в [15]).

Введем в рассмотрение следующие функционалы:

;

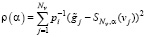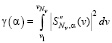. (14)

Тогда L-кривой (форма которой напоминает начертание латинской буквы L) называется параметрическая кривая с координатами (ρ(α), γ(α)). Можно показать, что кривизна L-кривой определяется следующей формулой:

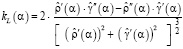, (15)

где 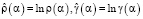. В качестве параметра сглаживания будем принимать величину αL, для которой кривизна kL(α) принимает максимальное значение.

Для вычисления значения кривизны по формуле (15) предлагается следующий подход (подробнее [15]):

1. Исходя из априорной информации задаются два крайних значения параметра сглаживания: минимальное – αmin; максимальное – αmax, между которыми должно находиться оптимальное значение αopt (например, αmin = 10–8, αmax = 102).

2. Между этими крайними значениями формируются (в логарифмическом масштабе) узлы αk, k = 1,…,Nα, в которых вычисляются значения функционалов 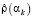, , 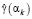k = 1,…,Nα (величина Nα выбирается в зависимости от «расстояния» между крайними точками αmin, αmax , например, Nα = 30).

3. По значениям 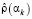, , 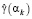αk, k = 1,…,Nα строят два интерполяционных кубических сплайна 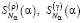, которые затем используются для вычисления первых и вторых производных функционалов 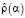, , 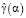входящих в формулу (15).

4. Используя численные методы одномерной оптимизации, вычисляют точку αL максимума кривизны kL(α).

В работе [15] выполнен обширный вычислительный эксперимент для ответа на вопрос: велик ли проигрыш по ошибке сглаживания при использовании αL вместо оптимального αopt, минимизирующего ошибку сглаживания 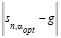, где 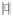– евклидова норма вектора, 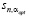– вектор, составленный из значений СКС в узлах сетки при оптимальном параметре сглаживания, вектор g составлен из значений точной функции в узлах сетки. Заметим, что в общем случае значение αopt можно определить только в вычислительном эксперименте, когда известны точные значения обрабатываемой функции. В качестве количественной меры эффективности параметра αL было принято отношение (названное коэффициентом эффективности)

,

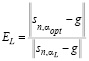где 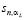– вектор, составленный из значений СКС в узлах сетки.

Очевидно, что чем ближе значения коэффициентов к 1, тем меньше проигрыш по точности параметра αL по сравнению с αopt. Так как EL является случайной величиной со значениями в интервале [0,1], то по выборке объемом 200 оценивались несколько числовых характеристик, одной из которых являлось среднее значение EL. Анализ этой характеристики, вычисленной для разных уровней шума и разных (по спектру) функций, показывает, что алгоритм выбора параметра сглаживания на основе метода L-кривой позволяет достаточно хорошо оценить оптимальное значение параметра сглаживания. Увеличение ошибки сглаживания при использовании параметра αL в среднем не превышает 5–15 % по сравнению с αopt.

Численное исследование предложенного алгоритма идентификации

Для определения точности предложенного алгоритма идентификации был выполнен следующий вычислительный эксперимент. В качестве тестовой идентифицируемой импульсной переходной функции нестационарной системы была взята функция, задаваемая выражением

.

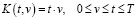Тогда

.

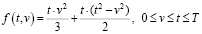Граница временного интервала T = 1, количество узлов Nt = 60, Nv = 70. На рис. 1 показана поверхность функции K(t,v).

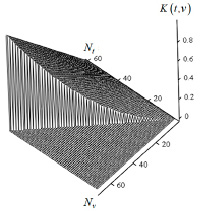
Рис. 1. Поверхность идентифицируемой функции K(t,v)

Первоначально определим методическую ошибку алгоритма идентификации. Для этого в узлах ti , i = 1,…,Nt vj, j = 1,…,Nv была вычислена матрица F с элементами 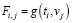размером 60×70. Эта матрица являлась исходной для предлагаемого алгоритма идентификации. Так как эти исходные данные принимались как точные, то вместо СКС строились интерполяционные кубические сплайны с краевыми условиями (10). На рис. 2 сплошной линией показаны значения функции K(t,v) (точное ядро) при t = 0.831, а точечной кривой – оценка 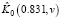, вычисленная по интерполяционным сплайнам 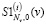, 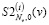. Относительную ошибку идентификации определим, как

,

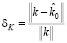где 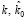– векторы, составленные из значений 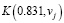, 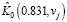соответственно. В этом эксперименте δK = 0.008. В экспериментах при других значениях аргумента t были получены относительные ошибки порядка 1 %. Поэтому можно сделать вывод, что предложенный алгоритм идентификации имеет низкую методическую ошибку.

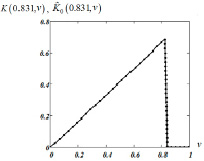
Рис. 2. Результаты идентификации по точным исходным данным

Рассмотрим влияние шумов измерения функции f(t,v) на точность идентификации. Для этого значения вектора 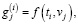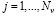, искажались нормально распределенным шумом ηj с нулевым средним и относительным уровнем

,

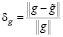где 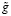– «зашумленный» вектор, составленный из значений

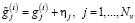. (16)

Сформированный таким образом вектор 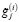использовался в качестве исходных данных для ранее описанного алгоритма идентификации. Параметры сглаживания α1(i), α2(i) сплайнов 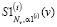, 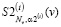вычислялись описанным выше алгоритмом метода L-кривой. На рис. 3 сплошной кривой нанесены точные значения 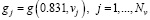, а точечной кривой – зашумленные значения 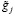, (16), относительный уровень шума равен 0,02. На рис. 4 сплошной кривой показаны значения K(0.831,v), а точечной кривой – оценка 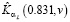, построенная по этим зашумленным значениям. Относительная ошибка идентификации δK = 0.038. Небольшие отклонения вычисленной оценки в начале и конце интервала можно объяснить влиянием задаваемых естественных краевых условий (14), которые отличаются от значений точной второй производной в крайних точках интервала построения сплайна. В сглаживающих сплайнах это влияние более выражено по сравнению с интерполяционными сплайнами.

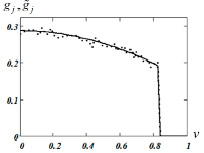
Рис. 3. Точные и зашумленные данные для построения оценки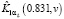

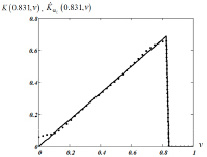
Рис. 4. Функция K(0.831,v) и ее оценка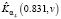

В качестве точностной характеристики алгоритма идентификации примем относительную ошибку идентификации δK. Средние значения δK этой случайной величины были вычислены по выборке объемом 50 и приведены в таблице для разных уровней шума измерения.

Относительные ошибки идентификации для разных уровней шума

Анализ данных таблицы показывает высокую устойчивость предложенного алгоритма идентификации к шумам измерений выходного сигнала идентифицируемой системы.

Заключение

В работе для кусочно-линейных входных сигналов предложена формула обращения, являющаяся основой для построения вычислительного алгоритма идентификации линейных нестационарных динамических систем. Использование сглаживающих кубических сплайнов позволило построить эффективный численный алгоритм идентификации с низкой методической ошибкой и хорошей устойчивостью к шумам измерения, а также вычислять устойчивое численное решение задачи идентификации по данным, зарегистрированным в узлах как равномерной, так и неравномерной сетки по переменной v.

Изложенный алгоритм идентификации на основе сглаживающих кубических сплайнов использовался для решения задачи моделирования динамики работы теплотехнического оборудования на локальном участке пароводяного контура энергоблока Назаровской ГРЭС, которая является одним из крупнейших производителей электроэнергии в Восточной Сибири и на Дальнем Востоке России [1].