Основными задачами, которые решаются при проектировании технологических процессов механической обработки, являются: определение способа отделения материала от заготовки, условий обеспечения свойств материала и геометрической формы [1]. Геометрический образ детали можно представить в виде множества различных поверхностей, взаимосвязанных между собой. Практически любую сложную поверхность можно аппроксимировать совокупностью элементарных поверхностей, к которым авторы относят цилиндр, плоскость, сферу [1].
Для представления геометрической формы деталей с учетом состава поверхностей и структуры их взаимосвязей в работе предлагается использовать отображение положения каждой поверхности в трехмерном пространстве в виде шестимерного вектора с указанием фиксируемых степеней свободы {Xl, Yl, Zl, Xα, Yα, Zα} [1]. При этом необходимо комплексно рассматривать весь комплекс размерных связей между поверхностями одновременно для всех указанных степеней свободы. Взаимосвязи между поверхностями удобно представлять в виде графов, где вершины графа – это элементарные поверхности, а ребра – размерные связи. Тогда с учетом требований к размерным связям в пределах каждой степени свободы имеем связный и ациклический граф или остовное дерево [2]. Полное число вариантов определяется с помощью формулы А. Кэли как количество остовных деревьев в полном графе на n вершинах равно nn-2 [3, 4].
На рис. 1, а, показана деталь, геометрическая форма, которой определяется как замкнутая часть пространства, ограниченная пересечением семи поверхностей. Положение каждой элементарной поверхности детали (рис. 1, а) представлено в виде шестиклеточной таблицы, характеризующей фиксацию (обозначена единицей) соответствующей степени свободы (рис. 1, б) [4, 5]. В соответствии с формулой Кэли общее количество вариантов корректной расстановки размерных связей, определяющих положение каждой поверхности, составляет 2 250 000.
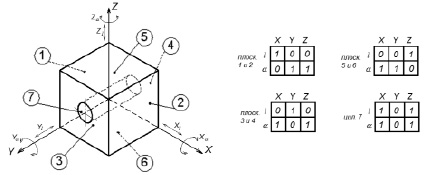
а) б)
Рис. 1. Конфигурация объекта с обозначением поверхностей (а); представление положения поверхностей в виде шестиклеточных таблиц (б)
Не всегда варианты расстановки (структуры) размерных связей обеспечивают сходимость алгоритма формального синтеза схем обработки детали, при условии последовательного использования обработанных поверхностей в качестве технологической базы [4, 6, 7].
Постановка задачи и исходные условия
При выполнении исследований задача заключалась в проверке сходимости алгоритма формирования последовательности смены комплектов баз для ряда вариантов задания размерных связей между поверхностями геометрического объекта в трехмерном пространстве.
В качестве метода исследования выполнялось моделирование процесса обработки с помощью алгоритма направленного поиска реально существующих сторон, которые могут быть использованы в качестве баз для ориентации детали при обработке её поверхностей [1].
Условиями, ограничивающими пространство поиска решений в рассматриваемой задаче, являются следующие постулаты:
1) при обработке детали можно использовать не более 3-х черновых баз;
2) используемые черновые базы должны быть смежными (непосредственно связанными размерной связью) с обрабатываемыми поверхностями;
3) любую черновую базу можно использовать один раз;
4) фиксируемые черновыми базами совокупности степеней свободы не могут пересекаться (повторяться).
В качестве исходного геометрического объекта для исследований использовался образ детали с размерными связями между поверхностями, показанный на рис. 2, а. Графы размерных связей для конфигурации этой детали изображены на рис. 2, б. Отметим, что любой граф с индексом α α из числа Xα, Yα, Zα (угловые размерные связи) является результатом исключающей суммы двух не одноимённых графов с индексом l (линейные размерные связи), например, граф в направлении Yα получается как сумма графов Xl, и Zl, с исключением повторяющейся вершины 7 и всех инцидентных ей связей (рис. 2, б) [1, 4].
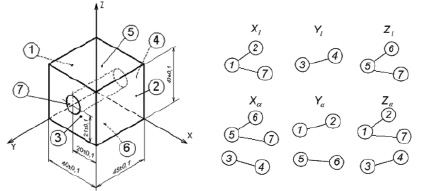
а) б)
Рис. 2. Деталь с нанесенными координирующими размерами (а) и соответствующие графы размерных связей (б)
На рис. 2, б, видно, что все графы в направлениях Xα, Yα, Zα несвязны, причем отсутствуют связи между взаимно перпендикулярными комплексами поверхностей, что исключает использование формальных алгоритмов поиска схем обработки детали. Поэтому указанные графы необходимо превратить в графы деревья [1, 2]. Для этих целей существует несколько вариантов. Так, в направлении Xα можно указать 6 вариантов простановки недостающей связи, в направлении Yα – 4 варианта и в направлении Zα – 6 вариантов.
В статье описываются результаты исследований поиска комбинаций структур размерных связей, обеспечивающих сходимость алгоритма формального синтеза схем обработки детали.
Моделирование смены баз при обработке поверхностей детали
Процедура моделирования обработки сторон детали и, соответственно, определения последовательности смены комплектов баз заключается в последовательном «переводе» обрабатываемых сторон из состояния необработанных (несуществующих) в состояние обработанных (реально существующих). Информационной основой для определения возможности обработки той или иной поверхности служит комплекс размерных связей по всем шести степеням свободы в трехмерном пространстве.
Первоначально весь комплекс поверхностей от 1 до 7 является необработанным, что не позволяет использовать какие-либо из указанных поверхностей в качестве исходных баз. Поэтому для моделирования процесса обработки поверхностей детали добавим дополнительно три черновых поверхности 2, 3 и 5 ч (условно параллельных обрабатываемым поверхностям с соответствующими номерами 2, 3 и 5), которые связаны размерами с поверхностями 1, 4 и 6 соответственно.
С учетом того, что каждая из черновых плоскостей 2, 3 и 5 ч может обеспечить фиксацию 3-х степеней свободы, суммарное количество базирующих точек получится равным девяти, в то время как в трехмерном пространстве существует только шесть степеней свободы и, соответственно, шесть базирующих точек (связей). Исходя из того, что две любые взаимно перпендикулярные плоскости при условии обеспечения полной определенности базирования конкурируют между собой при фиксации поворота вокруг линии их пересечения и могут лишить объект только пяти степеней свободы, необходимо выбрать, какая из этих плоскостей должна фиксировать три, а какая только две степени свободы [1].
Принцип формирования последовательности обработки показан на примере структуры размерных связей, представленной на рис. 3. Пунктиром обозначены связи, добавленные в граф, изображенный на рис. 2, б.
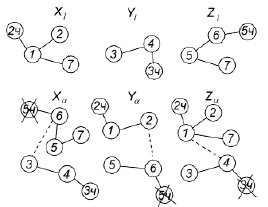
Рис. 3. Графы размерных связей
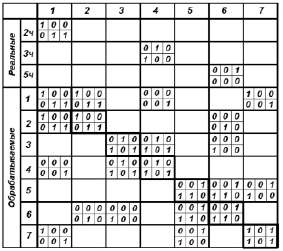
Рис. 4. Исходная матрица смежности
Процедура поиска решения заключается в последовательном рассмотрении столбцов матрицы до момента, когда поэлементная логическая сумма ячеек (необработанных поверхностей) матрицы совпадет с диагональной ячейкой [1].
На рис. 4 видно, что при использовании в качестве базы поверхности 2Ч можно получить поверхность 1. После обработки поверхности 1 столбец с номером 1 удаляется, а строчка переносится в верхнюю часть таблицы.
Далее, как видно на рис. 4, после получения поверхности 1 в столбце 2 появилась таблица, покрывающая диагональную, в столбце и строке с номером 2. Тогда использованием в качестве базы реальной поверхности 1, можно получить поверхность 2 и перенести полученную поверхность в верхнюю часть матрицы.
На следующем шаге, проверяя по столбцам соответствие шестиклеточных таблиц верхней части матрицы диагональным, можно видеть, что появляется соответствие в столбце 4. Здесь поэлементная логическая сумма реальных поверхностей 3 ч и 1 обеспечивает фиксацию, необходимую для получения поверхности 4. При получении поверхности 4 появляется совпадение в столбце 3, что позволяет получить поверхность 3, используя в качестве базы реальную поверхность 4.
На рис. 5 видно, что существует только один столбец с номером 6, в верхней части которого существуют шестиклеточные таблицы (5 ч, 2, 3), логическое сложение которых совпадает с диагональной ячейкой в стоке и столбце с номером 6. Таким образом, на следующем шаге имеется возможность обработки поверхности 6. Получение поверхности 6 позволяет получить поверхность 5, используя в качестве базы уже полученную реальную поверхность 6.
В столбце 7 существуют реальные поверхности 1 и 5, логическое сложение которых совпадает с табличкой в строке 7. Таким образом, смоделирована обработка последней поверхности, что означает сходимость алгоритма для рассмотренного варианта структуры размерных связей.
Аналогичным образом рассмотрены все возможные варианты расстановки размеров для обеспечения связности графов, показанных на рис. 3. Результаты моделирования показывают, что сходимость алгоритма обеспечивается только при условии наличия связей между вершинами, смежными с неиспользуемой черновой базой из числа конкурирующих в направлении поворота вокруг координатной оси.
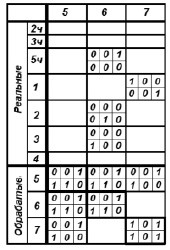
Рис. 5. Матрица смежности после 4 шага
Обсуждение результатов моделирования смены баз при обработке поверхностей
Процедура моделирования обработки сторон детали и определения последовательности смены комплектов баз была проведена для различных вариантов связей графов Xα, Yα, Zα и их сочетаний. В ходе проведения экспериментов было выявлено, что использование формальных методов синтеза комплектов баз и определения последовательности их смены возможно только при определенных сочетаниях графов Xα, Yα, Zα и их связей.
Алгоритм позволяет получить последовательность обработки поверхностей детали в случае наличия связи между вершиной, смежной с вычеркнутой черной поверхностью и вершинами графа, содержащего не вычеркнутую черную поверхность (рис. 3). Выявленная закономерность требует дальнейшего изучения и доказательства. Тем не менее полученный результат позволяет сделать следующий шаг в развитии теории формального синтеза технологического процесса изготовления деталей в машиностроении.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации по Государственному контракту № 02.G25.31.0173.
Библиографическая ссылка
Лелюхин В.Е., Игнатьев Ф.Ю., Колесникова О.В. ВЛИЯНИЕ СТРУКТУРЫ РАЗМЕРНЫХ СВЯЗЕЙ НА ФОРМИРОВАНИЕ ПРОЦЕССА ОБРАБОТКИ ДЕТАЛЕЙ // Современные наукоемкие технологии. – 2018. – № 7. – С. 60-64;URL: https://top-technologies.ru/ru/article/view?id=37079 (дата обращения: 26.04.2024).



