По трубопроводу диаметром 25×2,5 самотеком стекает нитробензол с температурой 20 °С. Начальная точка трубопровода выше конечной точки на 200 мм. Длина горизонтальной части трубопровода 240 м. Определить массовый расход нитробензола.
Имеем исходные данные: диаметр трубопровода: dн×δ = 25×2,5 мм (диаметр наружный толщину стен); длина трубопровода: l = 240 м; жидкость: нитробензол t = 20 °С; разность между начальной и конечной точками трубопровода h = 200 мм. Необходимо определить массовый расход нитробензола G [кг/с].
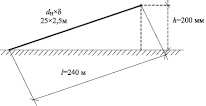
Расчетная схема трубопровода
Массовый расход жидкости определяется из формулы:
G = ω∙Fсеч∙ρ [кг/с],
где ω [м/с] – скорость нитробензола, неизвестна, F [м2] – площадь живого сечения потока, можно вычислить по формуле: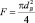 
, ρ[кг/м3] – плотность нитробензола, принимается из справочной литературы
Неизвестную величину, скорость нитробензола можно определить из формулы вычисления числа Рейнольдса:
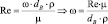[м/с], (1)
где µ [Па∙с] – коэффициент динамической вязкости нитробензола при t = 20 °С.
Однако точное значение числа Рейнольдса нам неизвестно. Предположим, что режим движения жидкости в случае безнапорного течения – ламинарный. Полный же напор жидкости обусловлен только линейными потерями и создается разностью высот конечных точек трубопровода h = 200 мм. Полный напор определяем из уравнения Дарси–Вейсбаха:
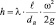[м],
где h = 200 мм = 200 [м].
Коэффициент сопротивления трения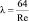 
– для жидкости, движущейся в прямой круглой трубке при ламинарном режиме движения.
Таким образом:
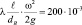
или
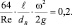(2)
Подставляем в уравнение (2) уравнение (1), получаем
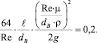
Раскрываем скобки:
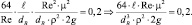
Подставляем
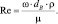
Получаем
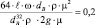
или
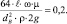
Определяем скорость движения из формулы:
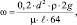
где
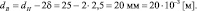
Подставив исходные данные, имеем:
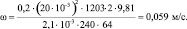
Таким образом, получаем массовый расход нитробензола:
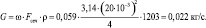
Библиографическая ссылка
Коротеева Е.А., Мокрецова И.С., Ребро И.В., Мустафина Д.А. Аналитический метод математического расчета массового расхода нитробензола // Современные наукоемкие технологии. – 2013. – № 6. – С. 104-105;URL: https://top-technologies.ru/ru/article/view?id=32008 (дата обращения: 03.12.2024).