целью данной работы является исследование электрического взрыва плоской кольцевой фольги и оценка амплитуды давления генерируемых ударно-акустических волн.
Электрический разряд в конденсированных средах представляет собой уникальное явление, одними из аспектов которого является скоротечность процесса и эффек- тивность воздействия на обрабатываемый объект. История генерирования и использования высокоскоростного выделения энергии электрического поля относится к 60-м годам прошлого столетия [1]. Широкий спектр физических эффектов, сопровождающих электрический взрыв проводников — генерация электромагнитных излучений, формирование ударно-акустических возмущений, получение наноразмерных порошков и т.д. — находят многостороннее применение в фундаментальных исследования и технологических процессах, поэтому требуют проведения дальнейших научных исследований для получения достоверной информации о физических свойствах наблюдаемых явлений [2 — 6].
Для того чтобы протекание процесса осуществлялось в согласованном режиме, т.е. при котором полная реализация энергии конденсаторного накопителя проис- ходила в первой половине периода разряда, необходимо выполнение ряда условий. условия оптимальности (1), часто цитируемые, удачные и убедительно согласующиеся с экспериментом в случае проводников в виде проволочек, эмпирически были получены автором [3], а также предложено выражение (2) для определения ℓсогл авторами [8]:
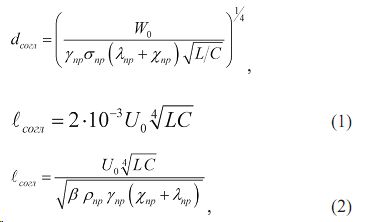
где dсогл, ℓсогл — диаметр и длина взрывающегося проводника, соответствующие протеканию разряда в согласованном режиме,W0 — запасенная энергия накопителя; U0 — начальное напряжение; С — емкость конденсаторной батареи; L — индуктивность разрядного контура; γпр,σпр — плотность и удельная электропроводность металлического проводника, λпр, Хпр — удельная теплота плавления и парообразования металла, β- коэффициент, зависящий от металла проводника, ρпр — удельное сопротивление проводника.
Определенный интерес вызывает электрический взрыв проводников, выполненных в виде плоского кольца из фольги [8], при котором разность потенциалов подается на центральную и периферийную ее части. Но в силу неоднородности распределения электрического поля в проводнике плотность разрядного тока j не является одинаковой вдоль радиуса. Для осуществления однородного электровзрыва при протекании тока в радиальном направлении необходимо, чтобы плотность тока j была одинакова по всему проводнику. А так как сила тока I в любом кольцевом сечении одинакова (рис. 1), то площадь сечения S(r) так же должна быть одинаковой; т.е. S(r) = 2πrh = 2πr1 h1 = 2πr2 h2 , тогда:
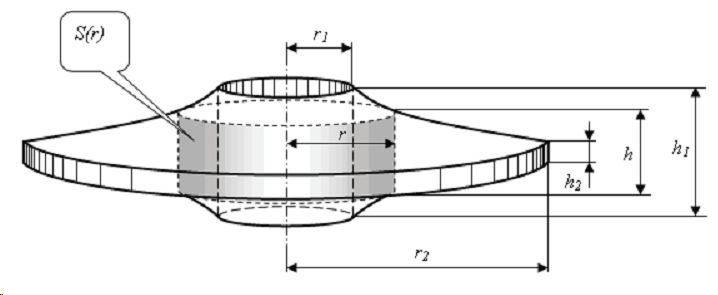
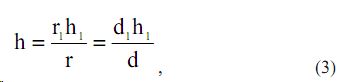
где d1=2r1 — внутренний диаметр кольца; d1=2r1 — внешний диаметр кольца; h1 — толщина на внутреннем диаметре; h2 — толщина кольца на внешнем диаметре. Как видно, толщина кольца по радиальному сечению должна иметь гиперболическую зависимость от радиуса h(r)~1/r. Сопоставляя кольцевую фольгу c системой радиально расположенных n цилиндрических проводников и принимая условие равенства объемов проводников Vц с размерами в соответствии (1) и (2) кольцевой фольги Vk с профилем (3) имеем:
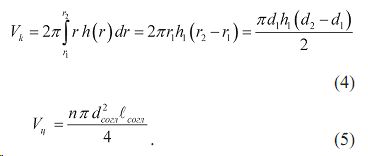
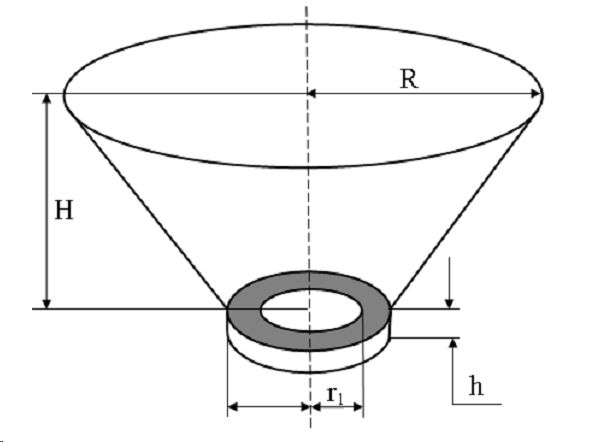
Приравнивая (4) и (5) получим высоту h1 центральной части:
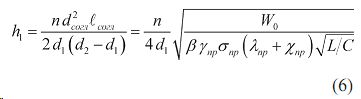
Использование предлагаемой геометрии взрывающегося проводника позволяет генерировать в окружающем пространстве плоскую ударно-акустическую волну [9]. Для оценки давления ударной волны плоскую кольцевую фольгу, имеющую малую толщину и незначительную разницу внешнего и внутреннего диаметров, предлагается рассматривать в качестве инициатора электрического разряда и не рассматривать физические процессы, протекающие в металлической фазе. Также считаем, что процесс протекания разряда является квазистатическим [10], т.е., время достижения максимального значения тока разряда на много больше времени прохождения звуковой волны до стенки камеры.
Далее следуя [10], имеем условие сохранения массы воды ρV´=const, где ρ — плотность жидкости в области между стенкой камеры и плазменным образованием; V´ — объем жидкости. Тогда:
Уравнение состояния жидкости представляется в форме Тэта:
где P — давление в камере равное давлению в канале разряда для квазистатического режима; для воды коэффициенты A=3.05·108Pa, α=7.15. Считаем, что объем жидкости, вовлеченной в процесс возмущения электрическим взрывом плоского кольца из фольги, представляет собой усеченный конус (рис. 4), объем которого определяется: 
, а также расширение плазменного образования происходит;
только вследствие увеличения высоты h, уравнение (7) сводится к виду:
,
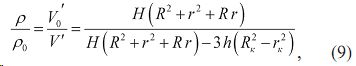
вводя обозначения
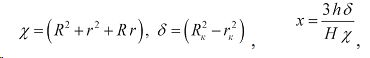
и подставляя в (8) получим для давления:
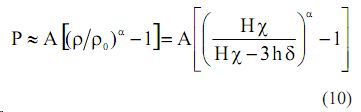
уравнение баланса энергии в канале разряда [11] представляется:
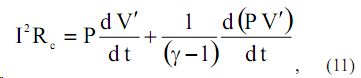
Вводя новую переменную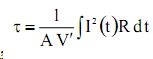 
, имеем:
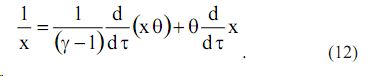
Решением уравнения (12) относительно τ является:
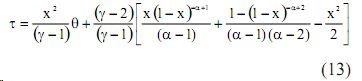
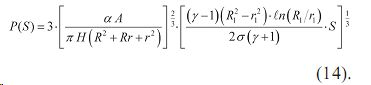
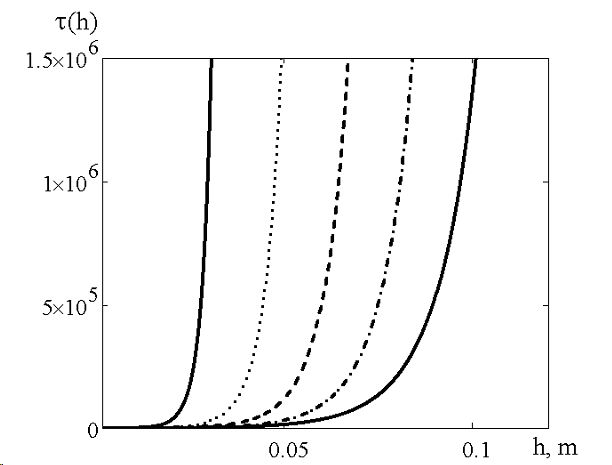
Используя начальные параметры взры- вающегося кольца и возмущенной среды rк=3·10 -3 м; Rк=7.5·10 -3 м; R=15·10 -3 м, выра- жение (13) позволяет определить величину объемной плотности энергии Е(h) переданной среде (рис. 5) в зависимости от из- менения высоты h=(0÷8)·10 -3 m плазменного канала, выполняющего роль поршня, при различных значениях высоты усеченного конуса H=(30÷120)·10 -3 m возмущенной среды.
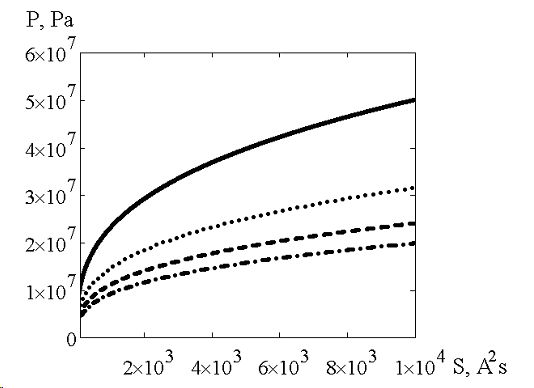
Выражение (14) позволяет оценить амплитуду давления ударно-акустической волны от интеграла действия S = ∫I2 (t)d t (рис. 6) при аналогичных значениях высоты H=(30÷120)·10 -3 m области возмущенной среды.
Список литературы
- Юткин Д.А. Электрогидравлический эффект. - М: Машгиз, 1955 - 51 с.
- Малюшевский П.П. Основы разрядноимпульсной технологии. - Киев: Hаукова думка, 1983. - 342 с.
- Кривицкий Е.В. Динамика электровзрыва в жидкости. - Киев: Наукова думка, 1986. - 205 с.
- Бурцев В.А., Калинин Н.В., лучинский А.В. Электрический взрыв проводников и его применение. - М: Энергоиздат,1990. - 217 с .
- Наугольных К.А., Рой Н.А. Электрические разряды в воде. - М: Наука, 1971. -155 с.
- Ушаков В.Я. Импульсный электрический пробой жидкостей. - Томск: Тгу,1975. - 256 с.
- Суркаев А.л., Кумыш М.М., Усачев В.И., Лысов Э.А. Силовая установка электрического взрыва металлических проводников в жидкой среде. // IV Межр-ная науч-прак. конф. »Взаимодействие ВуЗов и пром. пред-й для эффективного развития ин-ной деятельности« - Волжский,14.05.2008. С. 95-98
- Суркаев А.Л., Кумыш М.М. К вопросу об условиях оптимальности режимов электрического взрыва кольцевой фольги. ІI Межд-ная науч-практ. конф. «Дни науки - 2007» (апрель 2007 г.) www.rusnauka.com.
- Суркаев А.Л., Слепцов О.А. Электрогидроимпульсный способ запрессовки труб в труднодоступных местах. - пат. № 2125496. - 1999.
- Шнеерсон Г.А. Оценка давления при медленных режимах искрового разряда в цилиндрической камере, заполненной водой. // ЖТФ. 2003. т. 73. Вып. 3. С. 100-101.
- Наугольных К.А., Рой Н.А. Электрические разряды в воде. М: Наука, 1971. -155 с.
Библиографическая ссылка
А. Л. Суркаев, Ю .П. Муха, М.М. Кумыш ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ ЭЛЕКТРИЧЕСКОГО ВЗРЫВА ПЛОСКОЙ КОЛЬЦЕВОЙ ФОЛЬГИ // Современные наукоемкие технологии. – 2010. – № 6. – С. 83-88;URL: https://top-technologies.ru/ru/article/view?id=24965 (дата обращения: 03.12.2024).