В настоящее время широкое применение получили стохастические методы моделирования. Эти методы основаны на предпосылке, что система изначально содержит по меньшей мере один источник неопределенности. Стохастическое моделирование базируется на методах теории вероятностей и математической статистики [1–3]. Универсальным способом описания всякой случайной величины является функция распределения. Наиболее частыми распределениями, используемыми в моделировании, являются нормальное, логнормальное, экспоненциальное, равномерное, бета- и гамма-распределения. В стохастическом моделировании часто возникает задача нахождения обратной функции, например, для получения обратной зависимости переменных. В задачах стохастического моделирования функция, обратная к вероятностной функции распределения, может быть использована для получения ряда случайных чисел, соответствующих заданному закону распределения. В работах [4–5] показан метод и алгоритм получения аппроксимации обратной вероятностной функции, записываемой через ряд Тейлора.
В рамках данного исследования предполагается выполнить анализ возможности расширения математической библиотеки классов Mathphp. Данное расширение может быть использовано в задачах стохастического моделирования. При разработке вычислительных программ для решения задач стохастического моделирования могут использоваться как процедурная, так и объектно-ориентированная парадигмы [6, 7]. Объектно-ориентированный подход имеет неоспоримые преимущества и позволяет использовать готовые библиотеки классов. В данной работе показана разработка расширения математического класса, написанного на языке программирования php. Язык php создан для разработки онлайн-приложений. В качестве математической библиотеки выбрана библиотека MathPHP.
Материалы и методы исследования
MathPHP – мощная современная математическая библиотека, имеющая лицензию Массачусетского технологического университета MIT (официальный сайт https://github.com/markrogoyski/math-php). Библиотека MathPHP представлена различными разделами математики, в частности алгеброй, тригонометрией, численным анализом, матричной алгеброй, комплексными числами, полиномами, статистикой. В классе статистика реализованы различные вероятностные распределения. Класс функции наследует несколько классов. Один из них – класс Special. Класс Special описывает специальные функции, к которым относятся функция ошибок, бета, гамма, логистическая функция. Методы данного класса, как и других, имеют многострочный комментарий, описывающий вид функции, максимальную относительную погрешность представленной аппроксимации. Ниже показан путь к классу, представляющему функцию ошибок, используемую в задачах, решение которых связано с нормальным распределением:
math-php/src/Functions/Special.php
Метод, описывающий функцию erf, показан ниже:
public static function errorFunction(float $x): float
{
if ($x == 0) {
return 0;
}
$p = 0.3275911;
$t = 1 /(1 + $p * abs($x));
$a1 = 0.254829592;
$a2 = -0.284496736;
$a3 = 1.421413741;
$a4 = -1.453152027;
$a5 = 1.061405429;
$error = 1 – ( $a1 * $t + $a2 * $t ** 2 + $a3 * $t ** 3
+ $a4 * $t ** 4 + $a5 * $t ** 5 ) * exp(-abs($x) ** 2);
return ( $x > 0 ) ? $error : -$error;
}
Предложенная выше аппроксимация использует экспоненциальную функцию, являющуюся трансцендентной. Для решения задач, требующих высокой производительности, предпочтительным является использование алгебраических функций. Покажем реализацию метода erf_2_2 класса Special Functions, который представляет функцию erf в виде рациональной дроби в числителе и знаменателе которой стоят многочлены 2 степени.
На рис. 1 представлена блок-схема получения аппроксимации рациональной дробью [8]. Первый этап – получение разложения в ряд Тейлора. Для функции ошибок erf ряд Тейлора представляется следующим образом:
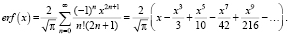 (1)
(1)
Используя алгоритм и программу, описанную в работе [8], получим аппроксимацию рациональной дробью с многочленом второй степени в числителе и знаменателе:
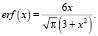 (2)
(2)
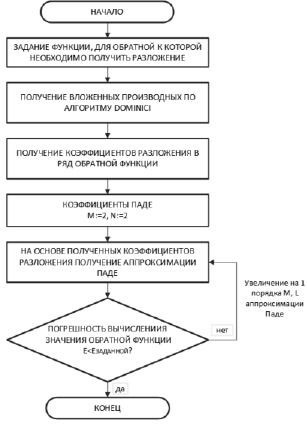
Рис. 1. Блок-схема получения коэффициентов аппроксимации Паде для функции обратной функции распределения
Расширим библиотеку добавив методы, описывающие функцию ошибок рациональной дробью. Для удобства использования методов класса продумаем нотацию методов. В названии метода к названию функции добавляются степени числителя и знаменателя. То есть для нашего примера рациональной дроби с многочленом 2 степени в числителе и знаменателе название запишется таким образом:
public static function erf_2_2(float $x): float
Ниже записан код метода erf_2_2:
public static function erf_2_2(float $x): float
{
if ($x == 0) {
return 0;
}
$error = 6*$t/(1.77245*(3+$t*$t));
return ( $x > 0 ) ? $error : -$error;
}
Для решения некоторых задач стохастического моделирования требуется генерация ряда значений, подчиняющихся заданному закону распределения. На рис. 2 показана схема метода, использующего генерацию ряда чисел, подчиняющихся нормальному распределению. Данный метод предназначен для оценки запаса углеводородов в пласте. Метод требует генерации большого количества случайных чисел, соответствующих нормальному распределению. В этом случае предпочтительными являются аппроксимации с использованием алгебраических функций.
Расширим данный класс, добавив методы, определяющие функцию, обратную к функции ошибок. Первым этапом необходимо получить разложение этой функции в ряд Тейлора. Ниже показано разложение функции erf–1(x), полученное в работе [5]:
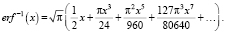 (3)
(3)
Следующий шаг алгоритма – получение рациональной дроби, в числителе и знаменателе которой стоят многочлены. Полученная аппроксимация представляет собой дробь с числителем и знаменателем 2 степени и имеет вид
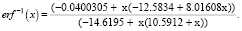 (4)
(4)
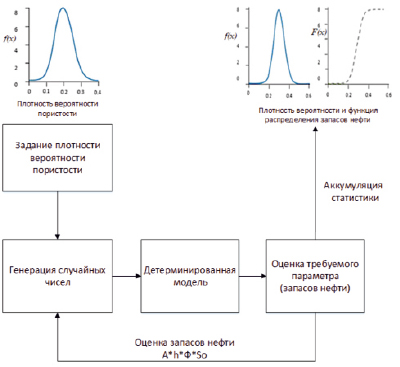
Рис. 2. Схема стохастического подхода при оценке запасов нефти в пласте
Запишем полученное выражение как метод класса MathPHP. В название метода добавим приставку inv_ и два числа в конце, разделенных нижним подчеркиванием, первое из которых степень числителя, а второе соответственно знаменателя. Ниже покажем код для аппроксимации функции, обратной к erf со степенью 2 в числителе и знаменателе дроби:
public static function inv_erf_2_2(float $x): float
{
$inv_error = (-0.0400305 + $x*(-12.5834 + 8.01608*$x))/(-14.6195 + $x*(10.5912 + $x));
return ( $x > 0 ) ? $error : -$error;
}
Для аппроксимации дробью со степенью 2 в числителе и 3 в знаменателе метод класса запишется следующим образом:
public static function inv_erf_2_3(float $x): float
{
$inv_error = (-0.0000699326 + (5.52147 – 4.53088*$x)*$x)/(6.23226 + $x*(-5.1401 +
$x*(-1.49546 + $x)));
return ( $x > 0) ? $error : -$error;
}
Для использования описываемых методов в технических приложениях необходимо знать погрешность аппроксимации. Посчитаем максимальную относительную погрешность для метода inv_erf_2_2 и добавим в многострочный комментарий к методу:
* Inverse Error function
* 2/2
* This is an approximation of the inverse error function
* (maximum relative error 0.7*10^?2)
* (-0.0400305 + x(-12.5834 + 8.01608x))
* erf^-1(x) ? -------------------------------------------
* (-14.6195 + x(10.5912 +x))
*
* @param float $x
*
* @return float
*/
Результаты исследования и их обсуждение
Разработанные в статье методы класса MathPHP представляют собой различные аппроксимации функции ошибок erf и обратной к ней функции erf_inv. Эта задача была решена с использованием алгебраических функций. Использование алгебраических функций является предпочтительным для решения задач стохастического моделирования, особенно требующих генерации огромного количества данных. Функции представлены рациональной дробью с полиномами в числителе и знаменателе различной степени. Алгоритм получения аппроксимаций рациональной дробью представлен на рис. 1. Для каждой реализации получены максимальные относительные погрешности. В зависимости от решаемой задачи и требуемой точности аппроксимации пользователь может выбрать необходимый метод библиотеки классов. Комментарии к коду методов содержат запись аппроксимации в привычной математической записи и информацию о максимальной относительной погрешности.
Заключение
Методы, дополняющие класс MathPHP, могут быть использованы для различных задач стохастического моделирования. Эти методы позволяют подобрать представление функций erf и erf_inv с допустимой для решения данной задачи относительной погрешностью.
Библиографическая ссылка
Богомолова О.И. РАСШИРЕНИЕ МАТЕМАТИЧЕСКОЙ БИБЛИОТЕКИ MATHPHP ДЛЯ РЕШЕНИЯ ЗАДАЧ СТОХАСТИЧЕСКОГО МОДЕЛИРОВАНИЯ // Современные наукоемкие технологии. – 2020. – № 12-1. – С. 9-14;URL: https://top-technologies.ru/ru/article/view?id=38404 (дата обращения: 23.04.2024).



