Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дьяков А.Н. 1 Кокарев А.С. 1 Пачин А.В. 1 Поляков С.А. 1

---

1 ФГБВОУ ВО «ВКА имени А.Ф. Можайского» МО РФ

Наличие достаточных комплектов запасных частей (ЗЧ) является необходимым условием для обеспечения надежности современной сложной техники. Однако при создании и эксплуатации мобильных технических средств существенным является ограничение на объемы возимых комплектов ЗИП. При этом не снимаются и ограничения по объемам ресурсов, выделяемых на приобретение ЗЧ. Одним из направлений создания систем обеспечения запасными частями (СОЗЧ), удовлетворяющих данным требованиям, является включение в их состав подвижных компонентов. В работе представлен подход к определению рациональных параметров подвижных СОЗЧ, входящих в состав мобильных сложных технических комплексов (МСТК). Методика позволяет с применением разновидности генетических алгоритмов – метода дифференциальной эволюции обосновывать решения, достаточные для практического применения при выполнении ограничений на габариты возимых запасов типовых элементов замены (ТЭЗ) и на стоимость комплектов запасных частей в системе в целом. При этом дополнительным ограничением, определяемым значительной размерностью задачи, является ограничение на объем вычислений, от которого зависит затрачиваемое машинное время. Методика может применяться как при разработке новых образцов МСТК, так и при управлении эксплуатацией существующих.

Статья в формате PDF

0 KB

мобильные сложные технические комплексы

подвижные системы обеспечения запасами

ЗИП

обеспечение надежности

метод дифференциальной эволюции

1. Кокарев А.С., Пачин А.В., Поляков С.А. Задача обеспечения запасами мобильных удаленных подразделений организации // VIII Уткинские чтения. Труды общероссийской НТК. СПб., 2018. С. 257–259.

2. ГОСТ 27.507-2015 Надежность в технике. Запасные части, инструменты и принадлежности. Оценка и расчет запасов. М.: Стандартинформ, 2017. 49 с.

3. Storn R., Price K., Differential Evolution a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization, Kluwer Academic. Publishers. 1997. Vol. 11. Р. 341–359. DOI: 10.1023/A:1008202821328.

4. Пантелеев А.В., Метлицкая Д.В., Алешина Е.А. Методы глобальной оптимизации. Метаэвристические стратегии и алгоритмы. М.: Вузовская книга, 2013. 244 с.

5. Pedersen M.E.H Tuning & Simplifying Heuristical Optimization: PHD thesis. University of Southapmton, 2010. 183 p.

6. Guliashki V., Toshev H., Korsemov Ch. Survey of Evolutionary Algorithms Used in Multiobjective Optimization. Problems of Engineering Cybernetics and Robotics. 2009. Vol. 60. Р. 42–54.

Одним из основных подходов к обеспечению надежности сложных технических систем является создание достаточных запасов ТЭЗ, предназначенных для оперативного устранения возникающих отказов. В значительной степени актуальна данная задача при обеспечении запасами ЗЧ современных МСТК а также различных удаленных подразделений [1], включающих значительное количество техники. Однако определяемые мобильностью дополнительные ограничения ведут к невозможности использования существующих моделей и методов [2] для обоснования параметров подвижных СОЗЧ.

Приведенные выше обстоятельства определяют актуальность исследования и позволяют сформулировать его цель – обеспечение требуемой надежности оборудования МСТК путем обоснования рациональных параметров СОЗЧ при комплексном учете габаритных и стоимостных ограничений.

Комплекс может быть представлен в виде моделей элементов, агрегатов и ЗИП. Использование полимодельных аналитико-имитационных комплексов позволяет получить зависимости показателей надежности каждого из агрегатов, входящих в состав МСТК, от показателей СОЗЧ – начальных уровней ТЭЗ в каждом ЗИП и периодичности пополнения, что позволяет перейти к решению следующей задачи.

Вербально задача сформулирована следующим образом: при известных структуре МСТК, номенклатуре, габаритных и стоимостных показателях ТЭЗ оборудования определить показатели СОЗЧ, обеспечивающей максимальные значения вероятности восстановления агрегатов комплекса и удовлетворяющей ограничениям по готовности каждого агрегата, объему возимых комплектов ЗИП и стоимость ТЭЗ.

Формальный вид задачи представлен ниже.

Дано:

I – количество агрегатов в МСТК;

J – количество типов ТЭЗ в оборудовании;

v_j – объем ТЭЗ j-го типа;

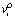– максимальный допустимый объем ЗИП-О i-го агрегата;

vA – максимальный допустимый объем ЗИП-А;

cj – стоимость ТЭЗ j-го типа;

C_Σ – максимальная допустимая стоимость всех ТЭЗ в СОЗЧ;

tвi – требуемое время восстановления работоспособности i-го агрегата;

t^Э – период эксплуатации;

Ω – величина популяции;

Т – число итераций алгоритма (поколений);

– требуемые значения коэффициента готовности для каждого агрегата;

K – состав оборудования агрегатов;

Δ – показатели наработки на отказ каждого типа ТЭЗ;

T – длительности перемещения ЗИП-А между эшелонами.

Найти:

.

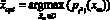Ограничения:

,

,

.

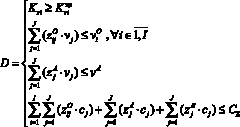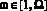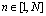Обоснование метода выбора задачи

Приведенные выражения позволяют оценить размерность поставленной задачи. Алгоритмическая зависимость показателей готовности и ремонтопригодности МСТК от показателей СОЗЧ учитывает влияние не целевые показатели множества различных параметров и является функцией, в которой количество переменных может достигать нескольких десятков. При этом переменные являются дискретными.

Применение классических методов математического программирования для решения подобных задач невозможно.

Наиболее перспективным подходом, позволяющим получить не абсолютно оптимальные, но обоснованные рациональные решения в заданных ограничениях, является применение генетических алгоритмов. Основанные на использовании эвристических подходов, данные методы не позволяют находить абсолютные экстремумы функции, однако, при сопоставимых объемах вычислений, позволяют получать более эффективные решения, чем иные методы стохастической оптимизации.

Одним из алгоритмов, реализующих концепцию генетических вычислений, является метод дифференциальной эволюции [3, 4]. Метод позволяет обрабатывать недифференцируемые, нелинейные, мультимодальные функции многих переменных. Он достаточно прост в реализации, содержит мало управляющих параметров, требующих подбора экспертами, и может быть реализован в алгоритмах, использующих параллельные вычисления. Основным преимуществом является отсутствие необходимости преобразования данных в двоичный вид, что при работе с целочисленными переменными позволяет существенно сократить объем вычислений [5, 6]. Приведенные преимущества определили выбор описанного метода в качестве основания для разработанной методики.

Общая схема вычислений

Алгоритмы, реализующие метод дифференциальной эволюции для поиска экстремумов функции множества переменных, включают общие для всего семейства генетических алгоритмов этапы:

а) создание начальной популяции векторов переменных путем генерации случайных значений. При этом размер популяции Ω является постоянной величиной, определяемой эвристически, а все созданные переменные должны принадлежать области допустимых значений;

б) итерационно над каждым вектором популяции выполняются операция мутации;

в) при выполнении операции скрещивания из каждого мутировавшего вектора получается вектор-потомок путем замещения некоторых компонентов вектора случайно сгенерированными. Замена компонента новым происходит с вероятностью ρ, являющейся одним из параметров алгоритма;

г) по значению целевой функции, получаемому от начального вектора и вектора-потомка, принимается решение о том, какой из них переносится в следующую популяцию.

Вычисления продолжаются итерационно до достижения критерия останова. Применительно к методу дифференциальной эволюции такими критериями могут быть:

а) достигнуто установленное число итераций алгоритма («поколений»);

б) полученное значение целевой функции, удовлетворяющее требованиям;

в) исчерпана установленная продолжительность выполнения вычислений;

г) значение целевой функции не улучшается в течение заданного числа повторений.

Полученные по окончании вычислений при приемлемых затратах машинного времени результаты являются квазиоптимальными и могут быть использованы в практических решениях.

Методика определения рациональных параметров подвижной СОЗЧ МСТК

Целью применения методики является получение обоснованных значений параметров СОЗЧ МСТК, обеспечивающей наилучшие готовность и ремонтопригодность оборудования при удовлетворении всех ограничений.

а) исходные данные

Исходными данными для выполнения расчетов являются количество агрегатов комплекса, период эксплуатации, требуемый коэффициент готовности, объем и стоимость ТЭЗ каждого типа, допустимые для каждого эшелона СОЗЧ объемы возимых ЗИП и максимально возможная стоимость всех запасов в системе в целом, размер популяции алгоритма дифференциальной эволюции и количество итераций (поколений), определяемое доступным машинным временем.

б) порядок использования методики

Схема выполнения вычислений представлена на рис. 1.

На первом этапе выполняется формирование начальной популяции векторов параметров СОЗЧ , являющихся аргументами функции, определяющей коэффициент готовности и вероятность восстановления за заданное время каждого агрегата. Элементы вектора – начальные уровни запасов каждого типа ТЭЗ в каждом эшелоне СОЗЧ 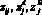и период пополнения ЗИП-А tПА. Элементы выбираются на основании равномерно распределенных в области допустимых значений случайных чисел. Область допустимых значений определяется:

а) для 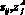– ограничениями на объем соответствующих возимых ЗИП и суммарной стоимостью ТЭЗ в СОЗЧ;

б) для tПА – заданным периодом эксплуатации.

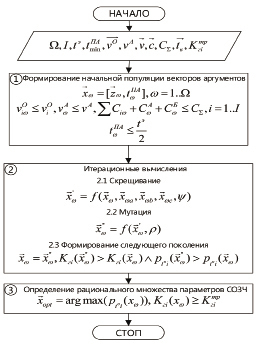
Рис. 1. Схема методики обоснования рациональных параметров подвижных СОЗЧ МСТК

Размер популяции Ω является одним из параметров алгоритма дифференциальной эволюции и определяется эвристически. Большие значения повышают вероятность нахождения более качественных решений, но увеличивают объем вычислений. В представленной методике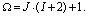

Второй этап вычислений по представленной методике включает следующие операции, выполняемые итерационно до достижения заданного числа поколений N:

а) получение вектора-мутанта. Для этого для каждого вектора из популяции случайным образом равномерно выбираются еще два отличающихся вектора и .

Затем рассчитываются значения компонент вектора-мутанта в соответствии с выражением .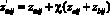

Если полученный элемент 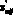не принадлежит области допустимых значений, то он заменяется случайным числом, равномерно распределенным в этой области.

Коэффициент χ = 0,5 определяет степень искажения мутировавшего вектора относительно исходного;

б) выполнение операции скрещивания (кроссовера). Для каждого из элементов вектора-мутанта выполняются генерация случайного числа, распределенного по равномерному закону 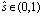, и замена элемента по правилу

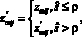
где ρ = 0,75 – параметр алгоритма, характеризующий вероятность изменения наследования вектором-потомком элементов исходного и вектора-мутанта соответственно;

в) формирование следующего поколения векторов осуществляется после определения значений целевой функции для исходного вектора 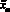и вектора 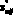, при этом дающий лучшее значение функции переходит в следующее поколение. Затем вычисления повторяются до достижения заданного числа поколений N.

Третьим этапом методики является определение рационального множества параметров подвижной СОЗЧ МСТК. Для этого из полученной последней популяции векторов параметров отбирается вектор 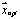, обеспечивающий выполнение требований по коэффициенту готовности каждого из агрегатов, при этом обеспечивающий наилучшее значение вероятности восстановления работоспособности агрегатов за заданное время;

г) результат применения представленной методики.

Результатом применения методики является набор оптимальных параметров подвижной СОЗЧ, обеспечивающей наилучшие показатели надежности, включающий в себя следующие компоненты:

а) начальные уровни запасов ТЭЗ каждого типа в одиночном комплекте ЗИП каждого агрегата ;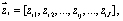

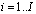б) начальные уровни запасов ТЭЗ каждого типа в групповом комплекте ЗИП-А и ЗИП-Б ;

в) период пополнения группового ЗИП-А из ЗИП-Б tПА;

г) пример расчетов.

С использованием представленной методики выполнен вычислительный эксперимент, позволяющий оценить возможность практического применения.

Дано:

I = 3; J = 3

v = [1, 2, 1, 3, 4], л

v_o = [50, 60, 70], л; vA = 100 л

с = [15, 20, 3, 1, 40], у.е. С_Σ = 900 у.e.

Δ = [0,02, 0,15, 0,11, 0,7, 0,12]•10-6, ч

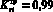t_вi ≤2

t^Э = 8460 ч Ω = 300 N = 20

На рис. 2 и 3 представлено графическое отображение хода процесса вычислений, выполненных.

Параметры СОЗЧ, полученные в результате вычислений, представлены в таблице.

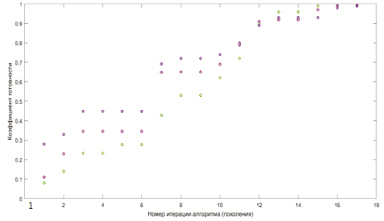
Рис. 2. Эволюционные изменения значений коэффициента готовности агрегатов

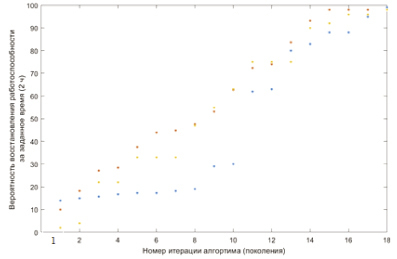
Рис. 3. Эволюционные изменения значений вероятности восстановления агрегатов

Рассчитанные рациональные параметры подвижной СОЗЧ МСТК

Построение СОЗЧ с полученными параметрами позволит обеспечить выполнение требований по готовности каждого из агрегатов комплекса, при этом обеспечить вероятность восстановления каждого агрегата за заданное время не менее 98 %. Вместе с тем выполнены требования по объемам возимых комплектов ЗИП-О и ЗИП-А и по стоимости всех ЗЧ.

Заключение

Представленная методика позволяет получать обоснованные решения как при разработке подвижных СОЗЧ вновь проектируемых МСТК, так и для оперативного управления эксплуатационными процессами на существующей технике.

Научная новизна полученного результата заключается в том, что применение представленной методики, в отличие от существующих, позволит в комплексе учитывать ограничения на объем возимых комплектов ЗИП при обосновании рациональных параметров подвижных СОЗЧ.

Практическая значимость представленного результата заключается в возможности получения обоснованных рациональных значений показателей подвижных СОЗЧ МСТК, обеспечивающих требуемое значение показателя готовности и наилучшее значение показателя ремонтопригодности при выполнении ограничений на объемы возимых запасов и стоимость ЗЧ.

Большая размерность представленной задачи определяет существенный объем вычислений, необходимых для получения результата, что, в свою очередь, обуславливает необходимость реализации указанной методики в виде программ для ЭВМ. Одной из реализаций является «Программа расчета рациональных параметров подвижной системы обеспечения запасными частями мобильных сложных технических комплексов», представленная авторами работы.

Библиографическая ссылка