Батанный механизм находится в числе наиболее нагруженных механизмов ткацких станков типа СТБ [1]. Батанный механизм служит для прибоя нитей утка и реализации процесса тканеформирования, а также для направления движения прокладчика, при прокладывании нити в зев [2]. Статистика учета простоев станков СТБ на предприятиях текстильной промышленности показывает, что 28 % простоев вызвано поломками элементов батанного механизма, при этом наиболее часто наблюдается выход из строя таких элементов, как батанный вал и бердо [1], из этого следует, что возникает необходимость учета динамических нагрузок на стадии проектирования, что позволит выявить необходимое количество упругих опор, в виде батанных коробок, для возможности беспрепятственного формирования ткани с заданными свойствами. Первым этапом динамического анализа является решение задачи о собственных частотах и формах колебаний бруса батана. Схема конструкции батанного механизма ткацкого станка типа СТБ, с учетом его рассматриваемых особенностей, приведена на рис. 1.
Приведенный на рисунке батанный механизм сконструирован следующим образом. Главный вал 10 и кулачки 9 получают вращение от привода станка. Через ролики 8 это движение преобразуется в возвратно-качательное движение двуплечих рычагов 6 подбатанного вала 5, а вместе с ним и лопастей 4, несущих брус 2 и бердо 1. Сопряжение профиля кулачков 9 таково, что при их повороте на некоторых угол батан во время пролета прокладчику утка через зев находится без движения в заднем положении, то есть имеет соответствующий выстой. Отдельные части подбатанного и главного валов, вращающиеся в подшипниках скольжения 11 и качения 12, соединены между собой муфтами 13. Кулачки 9 являются парными, то есть представляют собой кулачок и контркулачок с геометрически сопряженными профилями.
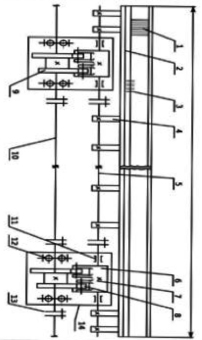
Рис. 1. Схема конструкции батанного механизма – вид со стороны грудницы станка
Цель исследования заключается в разработке методики математического решения задачи о формах и частотах свободных колебаний бруса батана ткацких станков типа СТБ с переменными граничными условиями и характеристиками податливости опор. В этой связи возникает необходимость учета динамических искажений кинематических функций батанного механизма, являющихся следствием упругой деформации его звеньев [3].
Одним из эффективных способов определения нагрузок, действующих на батанный механизм, является кинетостатический метод. В этой связи возникает необходимость учета динамических искажений кинематических функций батанного механизма, являющихся следствием упругой деформации его звеньев [3].
С целью определения частот свободных колебаний батанного механизма ткацких станков типа СТБ, происходящих на фазе подвода и уплотнения уточной нити, рассмотрим расчетную схему поперечного сечения элемента подбатанного вала, изображенную на рис. 2, построенную на основании рис. 1, где поперечные сечения обозначены mn и m'n', а длина подбатанного вала принята за dx. За обобщенный параметр движения принят угол поворота поперечного сечения, условно обозначаемый g (x, t). Зависимость обозначенного перемещения от координат сечения x и времени t, определяется связью угла поворота g (x, t) с крутящим моментом M поперечного сечения, определяется по формуле
M =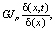 
(1)
где G – модуль сдвига, JP – полярный момент инерции сечения вала.
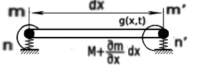
Рис. 2. Расчетная схема динамической модели бруса батана станка СТБ
На основании ранее проведенных нами исследований получены следующие математические модели. В смежном сечении крутящий момент определяется следующим образом:
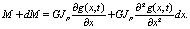(2)
Момент сил инерции элементарного участка вала длиной dx равен
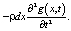(3)
Применяя принцип Даламбера, становится возможным выведение дифференциального уравнения движения элемента вала:
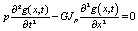(4)
которое преобразуем в
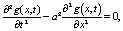(5)
где
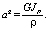(6)
Уравнение (5) относится к однородным дифференциальным уравнениям второго порядка в частных производных. Решение данного уравнения может быть выполнено по методу Фурье [4], в таком случае уравнение (5) будет представлено в следующем виде:
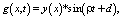(7)
где ρ – круговая частота собственных крутильных колебаний, а y(x) – функция координаты x, характеризующая изменение амплитуд крутильных колебаний по длине вала a – начальная фаза колебаний, то уравнение (7) будет отражать форму колебаний вала. В результате подстановки уравнения (7) в уравнение (5) и сокращения на sin(ρt + а) выводится стандартное дифференциальное уравнение:
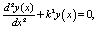(8)
где
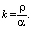(9)
Решение уравнения (8) выглядит следующим образом:
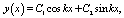(10)
где С1 и С2 – произвольные постоянные.
В случае, если на концах вала батана имеются две упругие опоры жесткостью С0, функция, определяющая формы колебаний, должна удовлетворять граничным условиям, которые имеют вид, при x = 0:
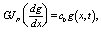(11)
при x = l
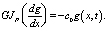(12)
Формы колебаний батана с двумя упругими опорами определяются посредством уравнения (8), после подстановки в него постоянных интегрирования С1 и С2, найденных из граничных условий (11) и (12), полученное выражение имеет вид
+
+ 
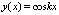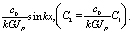(13)
Выполнение граничных условий (11) и (12) позволяет вывести систему однородных уравнений, применительно к коэффициентам С1 и С2.
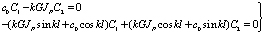(14)
С целью выведения уравнения для определения частот собственных колебаний, определитель данной системы необходимо приравнять к нулю, таким образом, получаем
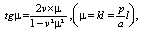(15)
где v – отношение жесткости вала батана к жесткости его опор
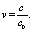(16)
При одной упругой опоре на правом конце вала и свободном левом конце (рис. 1) граничными условиями являются:
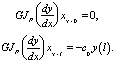(17)
Исходя из уравнений (8) и (17) выводим
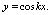(18)
Данное уравнение подходит для описания свободных колебаний батана с единой правой упругой опорой.
В случае, когда правый конец вала находится в свободном состоянии, а упругая опора расположена на левом конце, пограничные условия имеют следующий вид
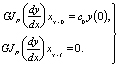(19)
Принимая условия уравнения (19) и взяв за основу уравнение (8), становится возможным определение форм свободных колебаний с одной левой упругой опорой:
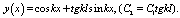(20)
При каждом рассмотренном варианте частное уравнение имеет следующий вид:
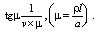(21)
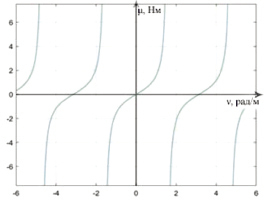
Рис. 3. Графическое решение частотного уравнения (15)
На рис. 3 представлено графическое решение уравнения (15) при различных значениях v. Как видно из приведенных графиков, увеличение v ведет к убыванию корня уравнения.
На основании сопоставления уравнений (15) и (21) с результатами расчетов, приведенных в работах других исследователей на смежную тематику [5], приходим к заключению, что при увеличении v корни уравнений (15) и (21) убывают. При v = 0 корнями уравнений (15) и (21) принимаем μ1 = π и μ1 =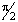 
.
В уравнениях (15) и (21), принимая величины μz, появляется возможность вычисления круговых частот колебаний по формуле
=
= 
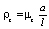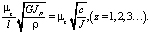(22)
В том случае, когда жесткость опор с0 в значительной мере превышает жесткость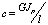 
подбатанного вала, динамическая модель батанного механизма с двумя коробками может быть представлена упругим подбатанным валом, защемленным по концам, с учетом момента инерции единицы длины 
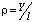. Уравнение форм и частотное уравнение для данного случая может быть получено из выражений (13) и (15). Приняв в формате данных выражений с0 = ∞, получаем
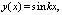(23)
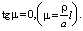(24)
Из уравнения (24) следует μz = zπ и частоты собственных колебаний следует
=
= 
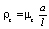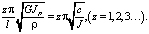(25)
Для механизма с одной батанной коробкой при с0 = ∞ динамическая модель имеет вид упругого вала, при условии, что масса распределена по длине, с защемлением одного конца вала, и свободного положения другого [6]. Уравнение форм в данном случае принимает вид (18) или (20), аналогично уравнениям вала с упруго закрепленным концом с правой или левой стороны. Частотное уравнение выводится из (21), в нем принимается v = 0 (c0 = ∞), отсюда:
tgμ = ∞ (26)
таким образом получаем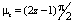 
и частоты колебаний:
= 
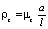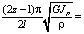
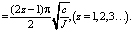(27)
В практических исследованиях наибольшее значение имеют первая, низшая или основная, частота колебаний упругой системы. При выражении батана в качестве упруго зафиксированного вала, приблизительное значение его частоты определяется по формуле, профессора Я.И. Коритысского [7]:
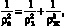(28)
где ρ0 – частота упруго зафиксированного вала; ρз – частота жестко зафиксированного вала; ρ – частота упруго зафиксированного жесткого вала.
При определении частоты собственных колебаний батана по формуле (28), батан должен быть представлен в виде совокупности двух систем упругой с жесткой фиксацией, жесткой системы с упругой фиксацией [8].
Частота колебаний системы с жесткой фиксацией для упругого вала, замещенного по концам, определяется по формуле (25) при z = 1 [9], таким образом, получаем
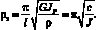(29)
Для упругого вала, один конец которого зафиксирован, а другой находится в свободном положении частоту колебаний системы с жесткой заделкой следует определять по формуле (27), при z = 1 получаем
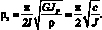(30)
Из уравнений (29) и (30), становится, очевидно, что во втором случае частота колебаний получается вдвое ниже [10].
Частота колебаний жесткой системы с упругой фиксацией определяется по формуле
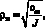(31)
где соз – суммарная жесткость опор батана на кручение.
Формула (28) позволяет без проведения натурных испытаний оценить воздействие отдельных динамических параметров на собственные частоты колебаний исследуемой системы, в частности оценить влияние на основную частоту колебаний батана жесткости подбатанного вала и жесткости его опор.
Для разработанной математической модели была составлена программа расчета на ЭВМ применительно к батанным механизмам ткацких станков СТБ-220 (рис. 4).
Использование разработанного программного обеспечения позволяет путем виртуального эксперимента определить возможность выработки на ткацком станке типа СТБ ткани с заданными параметрами. Это становится возможным за счет прогнозирования деформации бруса батана при различных вариантах количества и расположения батанных коробок, а следовательно, и производстве тканей заданного ассортимента. Применение данной методики повышает гибкость производства в плане быстрой смены ассортимента и может позволить избежать брака в процессе экспериментальной выработки новых артикулов ткани.
В результате применения приведенной методики, к батанным механизмам ткацких станков СТБ 220, были получены результаты, подтверждающие эффективность предложенной методики. В частности, на рис. 5 изображено графическое выражение форм собственных колебаний элементов батанного механизма станка СТБ-220.
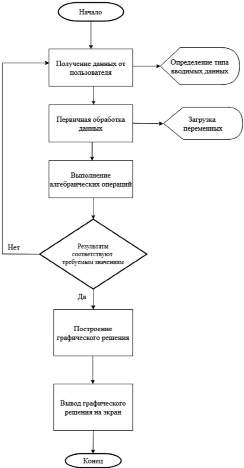
Рис. 4. Блок-схема разработанного программного обеспечения
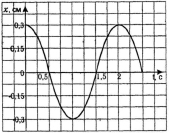
Рис. 5. Графическое изображение частотных колебаний
Выражения (13), (18) и (20), определяющие формы колебаний батана при различных граничных условиях, могут быть использованы для динамического анализа различных конструктивных схем, с учетом динамических искажений кинематических функций батанного механизма, являющихся следствием упругой деформации его звеньев. Использование данной методики на стадии проектирования батанного механизма позволит точнее определить, количество лопастей, а также количество и расположение упругих опор, что существенно повлияет на работу механизма и станка в целом.
Используя разработанное программное обеспечение для ткацкого станка СТБ-220, имеющего одну батанную коробку, были получены значения собственных частот p1 = 1374,9 с-1. При частоте вращения главного вала n = 260 об/мин его угловая скорость составляет ω = 24,5 с-1, следовательно, для всех собственных частот выполняются первичные условия гармоники ω ≤ p.
Результаты виртуального эксперимента, полученные с помощью разработанного программного обеспечения, позволяют упростить определение эффективности работы станка СТБ при заданном соотношении количества и расположения батанных коробок с параметрами вырабатываемой ткани, что предоставит возможность предотвращения отказа батанного механизма при недостаточном для производства ткани с заданными параметрами количестве батанных коробок.
Достоверность представленных в статье результатов, подтверждается логической непротиворечивостью с результатами более ранних исследований по данной тематике [11].
Выводы
1. Предложен способ математического решения задачи о формах и частотах свободных колебаний бруса батана ткацких станков типа СТБ, происходящих на фазе подвода и уплотнения уточной нити.
2. Получены дифференциальные уравнения для определения частотных характеристик батанных механизмов различных конструктивных моделей с переменными граничными условиями и характеристиками податливости опор.