Во многих областях производственно-экономической деятельности возникает необходимость в решении задач для определения максимального эффекта при заданных ограничениях на различные виды ресурсов [1]. Ввиду сложности современных объектов исследования для их модельного описания используются различные подходы, например – линейное программирование, частью которого являются транспортные задачи. В классическом варианте они ассоциируются с перемещением груза от поставщиков к потребителям. Решение данной задачи позволяет разработать наиболее рациональные пути и способы транспортирования товаров, устранить чрезмерно дальние, встречные, повторные перевозки. Всё это уменьшает стоимость доставки товаров, связанные с осуществлением процессов снабжения материалами, сырьём, оборудованием, топливом и т.д. Тем не менее алгоритмы и методы решения транспортной задачи могут быть использованы при рассмотрении других типов задач, не относящихся к классу объектов транспортировки груза, например сетевое, календарное планирование, составление расписания, оптимальное обеспечение материальными ресурсами предприятия, распределение торговых агентов и т.д. Известно, что при использовании методов линейного программирования необходимо выполнять многочисленные последовательные арифметические операции, причем ошибка на любом этапе решения приводит к неверному конечному результату, а повторные вычисления зачастую занимают много времени. Поэтому широкое практическое использование этой теории связано с появлением ЭВМ и соответствующего программного обеспечения.
При решении транспортной задачи используют стандартные программные средства (например, OpenOffice.org Calc, MS Excel, САПР MathCAD и др.) и специализированные программы (например, Lingo (demo-версия)), в том числе написанные на определенном языке программирования высокого уровня.
Как показал анализ литературы, например [1, 2, 6–10], ранее не проводилась оценка сложности в использовании и сравнительные характеристики современных программных средств для решения транспортных задач, что предоставило бы удобный инструмент для специалиста в области автоматизации такого рода вычислений для решения задач различного масштаба производственных и торговых предприятий. Поэтому рассмотрение способов решения транспортной задачи с использованием наиболее распространенных алгоритмических и программных средств с последующим их анализом является актуальной задачей и обладает научно-практической новизной.
Для решения поставленной задачи в качестве примера решим следующую типовую транспортную задачу. В трех пунктах отправления A1, A2 и A3 находится соответственно 34, 30 и 27 т горючего. Потребителям В1, В2, В3 и В4 требуется соответственно 25, 19, 29 и 21 т горючего. Стоимость перевозки одной тонны горючего из пункта А1 в пункты В1, В2, В3 и В4 соответственно 6, 2, 5 и 5 рублей за тонну горючего, из А2 – 4, 7, 3 и 6 руб., а из В3 – 2, 4, 1 и 5. Составить оптимальный план перевозок горючего так, чтобы общая сумма транспортных расходов была наименьшей (таблица).
План перевозок горючего
|
В1 |
В2 |
В3 |
В4 |
Всего |
|
|
А1 |
6 |
2 |
5 |
5 |
34 |
|
А2 |
4 |
7 |
3 |
6 |
30 |
|
А3 |
2 |
4 |
1 |
5 |
27 |
|
Всего |
25 |
19 |
26 |
21 |
Для решения этой задачи воспользуемся программой OpenOffice редактором CALC. Данный программный продукт является бесплатным аналогом пакета MicrosofOffice Excel и содержит необходимый инструментарий для построения математических моделей и решения задач линейного программирования (в том числе транспортных задач). Алгоритм работы следующий [2, 3]:
1. Введем исходные данные в ячейки рабочего листа OpenOffice.ORG редактор CALC;
2. Разметим блоки ячеек на рабочем листе OpenOffice.ORG редактор CALC, необходимые для моделирования объемов перевозок, а также для формирования элементов математической модели и целевой функции;
3. Сформируем на рабочем листе OpenOffice.ORG редактор CALC элементы математической модели и целевую функцию;
4. Настроим программу «Поиск решения» или «Решатель» (в зависимости от версии программы) и выполним ее.
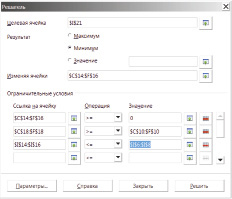
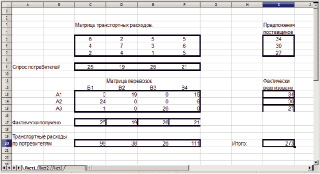
После выполнения пунктов 1, 2 и 3 получим рабочий лист OpenOffice.ORG CALC с размеченными блоками ячеек (рис. 1, а).

а)
б)
в)
Рис. 1. Решение транспортной задачи OpenOffice.ORG редактор CALC
5. Затем выберем из меню «Сервис» пункт «Решатель» и заполним поля в окне диалога программы (рис. 1, б).
6. После нажатия на клавишу «Решить» на рабочем листе получим решение нашей транспортной задачи (рис. 1, в).
Таким образом, можно сделать следующие выводы: решение транспортной задачи с помощью данного программного продукта имеет как ряд преимуществ, так и недостатков. К преимуществам можно отнести то, что OpenOffice.ORG CALC распространяется бесплатно и доступен любому пользователю, и за минимальное время возможно решить любую сбалансированную транспортную задачу. Недостатком является необходимость самостоятельной разработки пользователем математической модели, задание для нее ограничений и определение целевой функции, а это в свою очередь требует от пользователя математических знаний в данной области.
Теперь рассмотрим решение этой же задачи с помощью САПР MathCAD [2]. MathCAD – программное средство, среда для выполнения на компьютере разнообразных математических и технических расчетов, снабженная простым в освоении и в работе графическим интерфейсом, которая предоставляет пользователю инструменты для работы с формулами, числами, графиками и текстами.
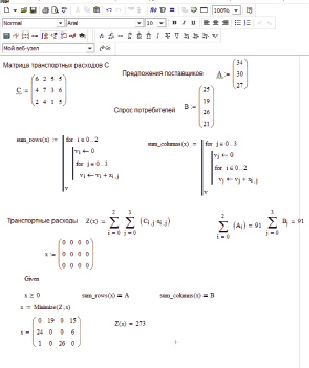
Рис. 2. Решение в MathCAD
При решении транспортной задачи в САПР MathCAD с помощью решающего блока необходимо (рис. 2):
1. Определить матрицу С и векторы a и b.
2. Сформировать функцию цели Z.
3. Задать матрицу начального приближения X.
4. В решающем блоке ввести ограничения, для этого необходимо сформировать массивы, в которых хранятся
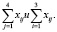
5. Решить задачу оптимизации с помощью функции Minimize [1].
В MathCAD доступны более сотни операторов и логических функций, предназначенных для численного и символьного решения математических задач различной сложности. Задача, решенная один раз, может быть использована для решения с другими исходными данными. Использование данного пакета имеет ряд недостатков: продукт является платным, пользователь должен уметь сам построить математическую модель. Сотрудник, работающий с системой, должен обладать навыками работы и программирования в данном пакете, что требует определенной подготовки специалиста.
Также задача может быть решена с помощью пакета Lingo [4], который является традиционным пакетом для решения задач линейного, целочисленного и квадратичного программирования (рис. 3, 4).
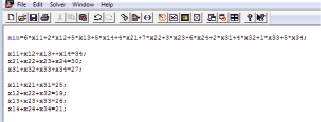
Рис. 3. Запись условия задачи в Lingo (demo-версия)
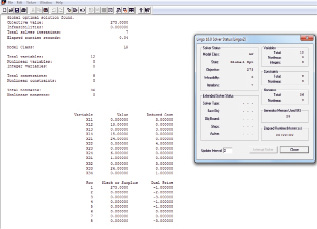
Рис. 4. Окно решения задачи в Lingo (demo-версия)
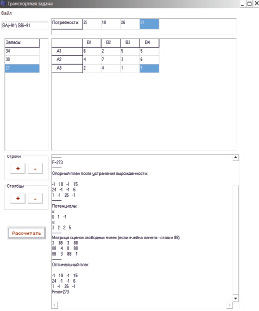
Рис. 5. Окно программы «Транспортная задача»
Несомненным преимуществом данного программного продукта является то, что модели в нем записываются в простой форме, соответствующей тому, как записываются уравнения на бумаге. В отличие от рассмотренных выше пакетов, Lingo позволяет решать несбалансированные (открытые) транспортные задачи. Из программных продуктов такого класса Lingo предлагает полный набор средств для изучения внутренней работы симплекс-метода, используемого для решения задач оптимизации линейных моделей. Также уникальным для Lingo является набор средств для целевого планирования, параметрического анализа, а также эффективного решения задач квадратичного программирования. Кроме того, полученные результаты позволяют проводить дальнейший анализ решаемой задачи. Несмотря на то, что доступна демо-версия пакета [5], полновесный пакет является платным.
Еще одним из вариантов является разработка программы самостоятельно. Например, написать на ЯВУ. Например, простейшая программа для решения транспортной задачи, разработанная в среде Delphi, будет выглядеть следующим образом (рис. 5). Программа реализует интуитивно понятный интерфейс и разработана для решения как транспортной задачи заданного условия варианта, так и для решения транспортных задач с другими исходными данными, удовлетворяющих условиям программы. Для ввода данных используется клавиатура. Данные, выводимые программой, соответствуют тем, что получены при расчетах вручную – методом наименьшего элемента и методом потенциалов, соответствуют решению в программах OpenOffice.org Calc, САПР MathCAD, Lingo (демо-версия).
Таким образом, в результате применения различных программных продуктов при решении предложенной задачи был получен одинаковый результат вычислений. Каждый из рассмотренных выше машинных способов решения имеет свои недостатки и преимущества в его использовании по сравнению с другими. К ним относятся, например, алгоритмическая сложность, полнота и системность функций обработки, стоимость, доступность продукта, а также время на подготовку специалиста для формирования навыков работы в рассматриваемых программных пакетах и др. Очевидно, что выбор того или иного программного продукта зависит как от возможностей пользователя, так и его целей. Проведенный анализ различных программных продуктов предоставляет возможность специалисту в сжатые сроки осуществить правильный выбор для автоматизации решения оптимизационных задач линейного программирования (на примере транспортной задачи) в зависимости от специфики технического задания.
Библиографическая ссылка
Приходькова И.В., Тарасова И.А., Авдеюк О.А., Поляков В.С., Наумов В.Ю., Павлова Е.С. АЛГОРИТМИЧЕСКИЕ И ПРОГРАММНЫЕ СРЕДСТВА ДЛЯ РЕШЕНИЯ ТРАНСПОРТНЫХ ЗАДАЧ // Современные наукоемкие технологии. – 2017. – № 7. – С. 66-71;URL: https://top-technologies.ru/ru/article/view?id=36731 (дата обращения: 19.04.2024).



