Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Нахушева Ф.Б. 1

---

1 ФГБОУ ВПО «Кабардино-Балкарский государственный университет им. Х.М. Бербекова» Министерства образования и науки РФ

Исследован вопрос однозначной разрешимости нелокальной задачи для нагруженного уравнения третьего порядка с кратными характеристиками.

Статья в формате PDF

972 KB

задача Бицадзе – Самарского

задача Коши

уравнение Вольтерра

функция Грина

1. Бицадзе А.В. Некоторые классы уравнений в частных производных. – М: Наука, 1981. – 448 с.

2. Джураев Т.Д. Краевые задачи для уравнений смешанного и смешанно-составного типов. – Ташкент: ФАН, 1979. – 238 с.

3. Елеев В.А. Краевая задача для смешанного уравнения третьего порядка параболо-гиперболического типа // Укр. мат. журнал. – 1995. – Т.47, № 1. – С. 20-30.

4. Елеев В.А., Кумыкова С.К. Внутреннекраевая задача для уравнения смешанного типа третьего порядка с кратными характеристиками // Известия Кабардино-Балкарского научного центра РАН. – 2010. – № 5. – С. 5-14.

5. Кумыкова С.К. Задача с нелокальными условиями на характеристиках для вырождающегося внутри области гиперболического уравнения // Дифференциальные уравнения. – 1981. – т. 17, № 1. – С. 81-90.

6. Нахушев А.М. Нагруженные уравнения и их применение. КБНЦ РАН/ – М.: Наука, 2012. – 232 с.

7. Нахушев А.М. Задачи со смещением для уравнений в частных производных. – М.: Наука, 2006. – 287 с.

8. Репин О.А., Кумыкова С.К. Об одной краевой задаче со смещением для уравнения смешанного типа в неограниченной области // Дифференциальные уравнения. – 2012. – т. 48, № 8. – С. 1140-1149.

9. Репин О.А., Кумыкова С.К. Задача со смещением для уравнения третьего порядка с разрывными коэффициентами // Вестник Самарского государственного технического университета. Серия: Физико-математические науки. – 2012. – № 4(29). – С. 17–25.

10. Репин О.А., Кумыкова С.К. О задаче с обобщенными операторами дробного дифференцирования для уравнения смешанного типа с двумя линиями вырождения // Вестник Самарского государственного технического университета. Серия: Физико-математические науки. – 2013. – № 1(30). – С. 150-158.

11. Репин О.А., Кумыкова С.К. О задаче с обобщенными операторами дробного дифференцирования для вырождающегося внутри области гиперболического уравнения. // Вестник Самарского государственного университета. Естественно – научная серия. – 2012. – № 9(100). – С. 52–60.

Теория краевых задач для уравнений смешанного типа, в силу теоретической и прикладной важности, является одним из интенсивно развивающихся разделов современной теории дифференциальных уравнений с частными производными и привлекает к себе внимание многих исследователей, интересующихся как самой теорией, так и ее приложениями. В частности, многие математические модели тепло- и массообмена в средах, окруженных пористой средой, сводятся к краевым задачам для уравнений смешанного типа.

Одним из важнейших классов уравнений с частными производными являются нагруженные уравнения смешанного типа. Исследованием локальных и нелокальных краевых задач для нагруженных и ненагруженных уравнений занимались авторы
[2 – 10]. Подробная библиография работ содержится в [6, 7].

Цель исследования: доказать существование и единственность решения нелокальной задачи для нагруженного уравнения третьего порядка с кратными характеристиками.

Постановка задачи.

Рассмотрим уравнение

(1)

где в конечной области Ω, плоскости переменных x и y, ограниченных отрезками AA0, A0B0, B0B прямых x = 0, x = l,
y = h соответственно и характеристиками AC: x + y = 0, BC: x – y = l уравнения (1).

Обозначим через и .

Задача. Найти функцию

,

удовлетворяющую уравнению (1) в  и условиям

(2)

(3)

(4)

где заданные функции, непрерывные в замыкании области их задания, причем .

Доказательство существования и единственности решения задачи.

Пусть и , где . Переходя в уравнении (1) к пределу при получим функциональное соотношение между , принесенное из области Ω1 на AB

(5)

В области Ω2 решение задачи Коши для уравнения (1) при имеет вид [1]

.

Удовлетворяя последнее условию (4) при , получим функциональное соотношение, принесенное из области Ω2 на линию АВ

(6)

Исключая из (5) и (6), получим следующую задачу для обыкновенного дифференциального уравнения третьего порядка

(7)

(8)

Задача (7) и (8) решается обычным методом вариации произвольных постоянных. По найденному t(x) определяется n(x) из соотношения (6) и решение задачи (1) – (4) в области Ω2 как решение задачи Коши.

После определения t(x) в области Ω1 приходим к задаче (1), (2) и , решение которой имеет вид [2]

(9)

где

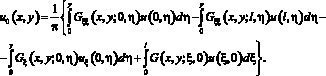
Функция Грина – представляется через фундаментальные решения, имеющие вид [2], [3]

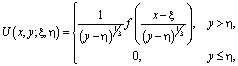
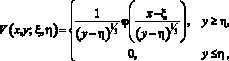
где

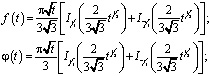
функция Бесселя, f(t) и j(t) – функции Эйри.

Удовлетворяя (9) условию (3), получим интегральное уравнение Вольтера второго рода относительно функции :

где ядро – выражается через известные функции, которое безусловно и однозначно разрешимо.

Пусть теперь . В этом случае решение уравнения (1) непрерывное в  с непрерывными производными до второго порядка включительно в Ω2 дается формулой [3]

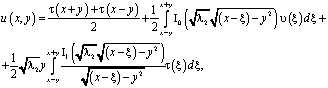(10)

где – функции Бесселя нулевого и первого порядков.

Удовлетворяя (10) условию (4), получим

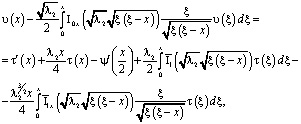(11)

где .

Уравнение (11) является уравнением Вольтерра второго рода относительно функции и его решение можно выписать с помощью резольвенты ядра в виде

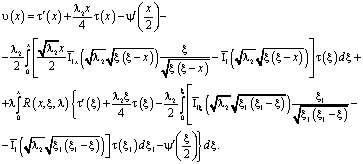
Подставляя значение функции u(x) в (5), получим обыкновенное дифференциальное уравнение относительно t(x):

,

где q(x), F(x) – выражаются через известные функции

,

,

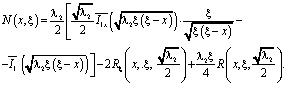
Интегрируя уравнение трижды от 0 до x с учетом (8), будем иметь

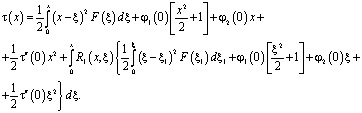
После определения t(x) в области Ω1 снова приходим к задаче (1), (2), решение которой дается формулой (9). В области Ω2 решение задачи определяется по формуле (10). Следовательно, решение задачи однозначно определяется в областях Ω1 и Ω2.

Библиографическая ссылка