Известно, что поверхностные физико-механические и физико-химические свойства материалов существенно отличаются от «объемных» показателей аналогичных свойств этих же материалов. Для кристаллов эти отличия в определенной мере определяются некоторыми особенностями строения приповерхностных 4-6-ти атомных слоев из-за близости межфазной границы, обладающей повышенной концентрацией структурных дефектов [1, 2]. Необходимо отметить, что возможные структурные состояния на поверхности кристалла генетически связаны со структурными состояниями в их объеме и, вероятно, полностью определяются ими. В связи с этим анализ возможных структурных состояний на поверхности кристаллических фаз, а также анализ связанных с ними проявлений аномальных геометрико-топологических характеристик, влияющих на чувствительные к ним свойства, в частности свойства модулярных структур [3-21], аномальную атомную плотность отдельных фрагментов или их возможный квазифрактальный характер на поверхности кристаллов [22-28], является актуальным.
Анализ вероятных структурных состояний поверхности кристаллических фаз основан на предположении о возможности проявления особенностей 3D структур на 2D сетке поверхностных атомов в некоторой локальной транзитивной области – переходной области, в которой реализуются особенности атомного строения на поверхности и в объеме кристалла. Таким образом, анализируемые структурные состояния в транзитивной области и их поверхностная концентрация в определенной мере могут служить аппроксимантами вероятных аномальных структурных состояний кристаллических материалов [20, 21, 24, 27, 28].
Сравнительный анализ структурных состояний проводили для R3 и R2 структур, вложенных в предварительно структурированные (ячеистые) 3D и 2D пространства. В данной работе предполагается, что возможна реализация по крайней мере двух механизмов проявления структурных элементов кубической ячейки (вершин, ребер, граней) (рис. 1) на квадратной сетке: механизм замещения структурных элементов 2D сетки и механизм внедрения в нее. Разная маркировка ребер и граней кубической ячейки означает возможные различия в ориентации реализуемых на них структурных состояний R3 структур.
![]()
Рис. 1. Кубическая ячейка 3D пространства и изображения ее ориентационно различных структурных элементов: ребер и граней
Некоторые результаты реализации этих механизмов представлены на рис. 2–4. Очевидно, что геометрико-топологические характеристики транзитивных областей в каждом случае существенно отличаются друг от друга.

Рис. 2. Фрагмент квадратной сетки (а) и некоторые варианты проявления 3D ячейки с помощью ее ребер и граней по механизму замещения центральной вершины (б) и по механизму симметричного внедрения в центральную область фрагмента (в)
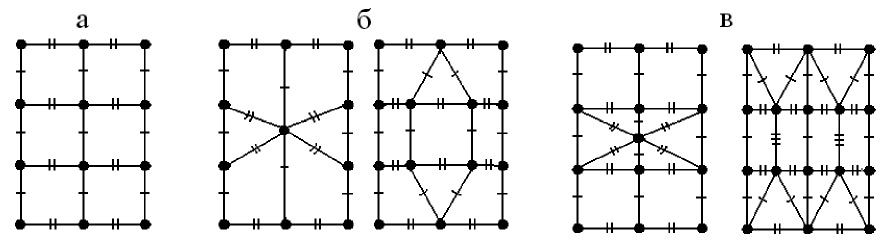
Рис. 3. Фрагмент квадратной сетки (а) и некоторые варианты проявления 3D ячейки с помощью ее вершин и граней по механизму замещения ребра (б) и по механизму симметричного внедрения в центральную область фрагмента (в)
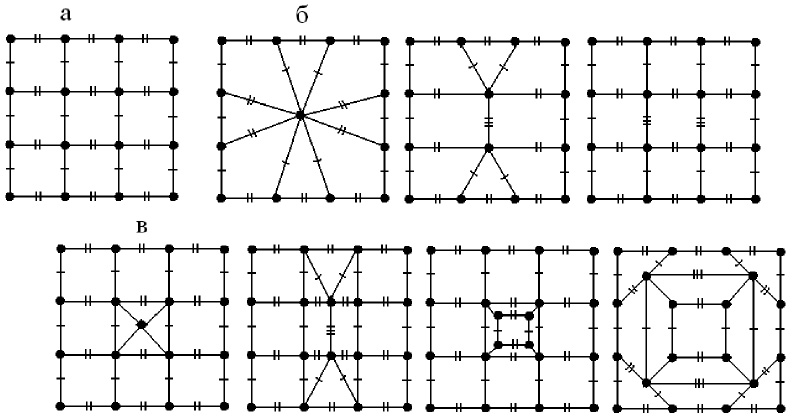
Рис. 4. Фрагмент квадратной сетки (а) и некоторые варианты проявления 3D ячейки с помощью ее вершин, ребер и граней по механизму замещения центрального квадрата (б) и по механизму симметричного внедрения в центральную область фрагмента (в)
Необходимо отметить, что одна из основных характеристик транзитивной области – ее площадь, существенно зависит от механизма и вида проявления структурных элементов кубической ячейки на сетке (табл. 1). В предположении о равенстве площади транзитивной области суммарной площади ячеек, из которых она была образована, можно сделать заключение о том, что практически во всех случаях (за исключением некоторых вариантов на рис. 3,б и 4,б) наблюдается аномальное увеличение атомной плотности.
Таблица 1
Площадь транзитивной области в зависимости от механизма и вида проявления кубической ячейки
|
Структурные элементы |
Площадь транзитивной области |
||
|
2D ячейки |
4D ячейки |
Механизм замещения |
Механизм внедрения |
|
вершина |
Ребро |
4 |
4 |
|
Квадратная ячейка |
4 |
4 |
|
|
ребро |
Вершина |
6 |
2 |
|
Ребро |
6 |
- |
|
|
Квадратная ячейка |
6 |
6 |
|
|
Квадратная ячейка |
Вершина |
9 |
1 |
|
Ребро |
9 |
3 |
|
|
Квадратная ячейка |
9 |
- |
|
Примечание. Площади транзитивных областей приведены в единицах ячеек квадратной сетки.
Проанализируем вероятные соотношения между R3-структурой и ее возможными подструктурами в 2D пространстве. Будем априори предполагать, что между геометрико-топологическими свойствами 3D ячеек и ее 2D подъячеек и такими же свойствами соответствующих модулярных R3 и R2 структур, вложенных в эти ячейки, существует морфизм соотношений. В этом случае любая 2D модулярная структура может быть подструктурой по крайней мере одной из модулярных 3D структур. Другими словами, любая 2D модулярная структура может иметь не одно структурное «продолжение» в дополнительном измерении и должна рассматриваться как результат определенного 2D сечения по крайней мере нескольких модулярных 3D структур.
Будем рассматривать возможные структурные состояния R2 структур как вероятные подструктуры определенной R3 структуры. При этом наряду с кристаллической компонентой состояния будем учитывать и фрактальную компоненту, предполагая также и возможность существования гибридных R3 структур [29]. В частности, кроме кристаллических структур вида R33r будем рассматривать еще две разновидности: детерминистических гибридных структур вида R32r,1f, и R31r,2f и детерминистические фрактальные структуры вида R33f
(табл. 2).
Таблица 2
Возможные структурные состояния R2 подструктур соответствующей R3 структуры
|
Возможные структурные состояния R3 структуры |
Возможные структурные состояния R2 подструктур |
|
Структура вида R33r |
|
|
(r, r, r) (r1, r1, r2) (r1, r2, r3) |
3 (r, r) (r, r) и 2 (r1, r2) 2 (r1, r1, r2) и 2 (r1, r2, r2) (r1, r2), (r1, r3) и (r2, r3) |
|
Структура вида R32r,1f |
|
|
(r, r, f) (r1, r2, f) |
(r, r) и 2 (r, f) (r1, r2), (r1, f) и (r2, f) |
|
Структура вида R31r,2f |
|
|
(r, f, f) (r, f1, f2) |
2 (r, f) и (f, f) (r, f1), (r, f2) и (f1, f2) |
|
Структура вида R41r,3f |
|
|
(f, f, f) (f1, f1, f2) (f1, f2, f3) |
3 (f, f) (f, f) и 2 (f1, f2) (f1, f2), (f1, f3) и (f2, f3) |
Примечание. r – кристаллическая, а f – фрактальная компоненты структурного состояния.
Из представленных в таблице 2 данных следует, что существует определенное многообразие проявления R3 структур в 2D пространстве. Например, структура вида R32r,1f формально имеет 3 разновидности R2 подструктур: R22 структуру и 2 вида R21r,1f структур. Аналогичный гетероморфизм существует и для R3 структур, в которых может реализоваться заданная R2 структура. Например, структура вида R22 может быть подструктурой как структуры вида R33r, так и структуры вида R32r,1f. Формально из предположения о возможности существования такого многообразия проявлений структур вытекает, что определенные гибридные кристалло-фрактальные R3 структуры в 2D пространстве могут выглядеть кристаллическими R2 структурами, и наоборот, некоторые кристаллические поверхностные R2 структуры в 3D измерении могут иметь фрактальное «продолжение» и быть подструктурами кристалло-фрактальной R32r,1f структуры.
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки N6.8604.2013.
Библиографическая ссылка
Иванов В.В., Таланов В.М. ВОЗМОЖНЫЕ ВАРИАНТЫ ПРОЯВЛЕНИЯ СТРУКТУРНЫХ ОСОБЕННОСТЕЙ 3D Р-ЯЧЕЙКИ НА 2D КВАДРАТНОЙ СЕТКЕ // Современные наукоемкие технологии. – 2013. – № 12. – С. 56-59;URL: https://top-technologies.ru/ru/article/view?id=33596 (дата обращения: 18.04.2024).



