В статье рассматривается разработка моделей и методов для поддержки высокопроизводительных вычислений, реализуемых на сетевом вычислительном ресурсе (информационно-исследовательская система ИИС MD-Slag-Melt»)[1], позволяющем исследовать структуру и свойства многокомпонентных шлаковых расплавов методами компьютерного моделирования, в том числе методом молекулярной динамики.
Принципиальное отличие систем, являющихся предметом исследования в ИИС, состоит в том, что это полимеризующиеся системы с многочастичным взаимодействием, объединяющим несколько видов взаимодействий: двухчастичные вклады (дальнодействующие ионные и близкодействующие отталкивательные) и многочастичные (двух и трех-частичные ковалентные взаимодействия).
Моделирование полимеризующихся ионно-ковалентных систем является нетривиальной задачей, требующей учета особенностей взаимодействия частиц в расплаве, что существенным образом усложняет постановку задачи распределения. Расчет математических моделей коррелированных систем, содержащих 105-107 частиц, требует разработки специальных методов для высокопроизводительных вычислений таких систем.
Авторами разработан ряд методов для поддержки высокопроизводительных вычислений, которые используют модель неоднородных дескрипторов для распределенного МД-моделирования коррелированной системы N-частиц [2, 3].
Основными элементами модели, обеспечивающими возможность распределения расчетов без детализации всех взаимодействий между частицами, являются объект и дескриптор. Под объектом понимается некоторая совокупность описаний частиц исходной системы, а также отношений между ними, выделяемая по определенным правилам и обеспечивающая возможность декомпозиции системы для распределения и распараллеливания расчетов.
Объекты идентифицируются с помощью неоднородных дескрипторов, которые содержат разнотипные элементы описания выделенного объекта необходимые для распределения расчетов.
Авторами, на основе концептуальной модели МД-метода и тщательного анализа программного кода локального МД-приложения [4] построен набор дескрипторов, которые можно разделить по двум классам: одночастичные дескрипторы (D1s(i), D1v(i)) и агрегаторы (двух- и трех-частичные (D∑2(i), D∑3(i)) дескрипторы).
Таким образом, предложенный подход позволяет отвлечься от конкретного наполнения элементов дескрипторов, перенести акцент с описания физических взаимодействий в системе на информационное описание перераспределения потоков данных между дескрипторами. На основе этого подхода построена вычислительная модели распределенных вычислителей.
Для модели распределенных вычислителей, разработан метод равномерной загрузки вычислителей в однородной вычислительной среде [3].
Ниже описывается метод параллельного расчета коррелированной системы N-частиц на графическом процессоре, развивающий описанные подходы.
Применение вычислителей на основе графических процессоров (GPU) при параллельном расчете дескрипторов, позволит существенное уменьшить время моделирования системы N-частиц.
В методе учитываются особенности архитектуры графических процессоров NVIDIA, и технологии CUDA. Параллельный расчет выполняется большим числом нитей, сгруппированных в блоки. В отличие от вычислителей, реализующих расчеты на центральных процессорах, GPU содержит семь видов памяти, различающихся по размеру, возможности записи и скорости чтения. Графический процессор не выполняет параллельный расчет самостоятельно, функции запуска расчета, отслеживания хода выполнения расчета и передачи дескрипторов в память GPU, выполняет центральный процессор.
На рисунке представлен алгоритм параллельного расчета одночастичных дескрипторов на GPU.
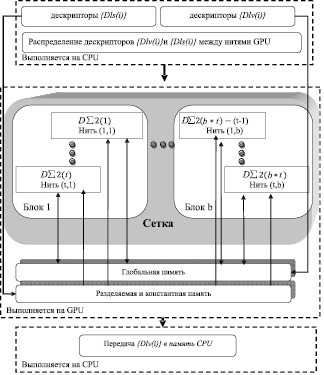
Алгоритм параллельного расчета одночастичных дескрипторов на GPU
Все множество значений элементов дескрипторов {Dlv(i)} передается в глобальную память (обладает большой вместимостью) GPU, из-за большого количества передаваемых данных. В константную и текстурную память передаются дескрипторы {Dls(i)}, что позволяет разгрузить глобальную память.
Центральный процессор формирует специальную сетку, состоящую из блоков (b), в которых определяется количество нитей (t) необходимых для расчета. Разделение множеств дескрипторов на подмножества и передача их на нити реализуется с помощью метода равномерной загрузки вычислителей.
Каждая нить производит расчет одного двухчастичного DΣ2(i) агрегатора и на основе полученных результатов обновляет значения элементов одночастичные векторные дескрипторы.
Для расчета двухчастичных {DΣ2(i)}агрегаторов на графическом процессоре применяется алгоритм «диагональной матрицы». Так как память для всех вычислителей одна, то возможны конфликты записи, когда вычислители обращаются к одному и тому же значению элемента дескриптора. Для этого на каждой итерации результат расчета значений элемента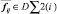 
передаются в специальный двумерный накопитель. Так же на каждой итерации цикла производится синхронизация. Расчет будет возобновлен только после прохождения одной итерации расчета значений элемента 
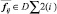всеми нитями.
Для оценки эффективности разработанного метода проведен ряд экспериментов связанных с расчетом коррелированной системы N-частиц. В экспериментах сравнивается время, затраченное на проведение локального варианта расчета коррелированной системы N-частиц и параллельного расчет с использованием технологии CUDA. Дескрипторы заполняются тестовыми значениями элементов. Тестирование модели, в основе которой заложен расчет с использованием технологии CUDA, проведено на графическом процессоре GForceGTS 450. Результаты компьютерных экспериментов представлены в таблице.
Результаты компьютерных экспериментов коррелированной системы N-частиц
|
Локальный вариант |
CUDA |
|||||
|
Количество частиц в системе |
50176 |
250880 |
401408 |
50176 |
250880 |
401408 |
|
Время расчета в секундах |
7,6 |
180,4 |
548,2 |
0,14 |
3,53 |
9,11 |
Согласно результатам тестирования серьезное ускорение наблюдаются при расчете системы на графическом процессоре GTS 450. Так же в модели параллельного расчета коррелированной системы N-частиц для графического процессора заложены процедуры позволяющие хранить данные в быстрой разделяемой и константной памяти GPU, что существенно сокращает время проведения моделирования.
В настоящее время модель распределенных вычислителей проходит апробацию в программном комплексе ИИС «MD-SLAG-MELT»[5]
Библиографическая ссылка
Трунов А.С., Воронова Л.И., Шалабай Т.С. МЕТОД ПАРАЛЛЕЛЬНОГО РАСЧЕТА КОРРЕЛИРОВАННОЙ СИСТЕМЫ N-ЧАСТИЦ НА ГРАФИЧЕСКОМ ПРОЦЕССОРЕ // Современные наукоемкие технологии. – 2013. – № 6. – С. 117-119;URL: https://top-technologies.ru/ru/article/view?id=32020 (дата обращения: 21.11.2024).