Активно развивающиеся в последние годы модели и методы высокопроизводительных вычислений имеют широкую область применения, в том числе и для поддержки научного компьютерного эксперимента.
В рамках компьютерного моделирования можно выделить важный класс задач, в которых возможно распределять вычисления для совокупности объектов, находящихся в определенных отношениях друг с другом. К этому классу относятся и задачи моделирования коррелированных систем N-частиц.
В настоящее время разработан ряд программных комплексов реализующих методы распределенного расчета задач класса N-частиц [1-3]. Эти методы основаны на расчете двухобъектных отношений [4, 5]. Предметом этой статьи являются методы, основанные на двух объектных отношениях с учетом трехобъектных и многообъектных отношений [6, 7].
Для возможности параллельного расчета коррелированной системы N-частиц, авторами разработан метод равномерной загрузки вычислителей в однородной вычислительной среде, в которой каждый вычислитель обладает одинаковой производительностью и имеет свою независимую память.
Равномерная загрузка подразумевает разделение множества на подмножества с мощностью равной k = N/p, где N количество одночастичных дескрипторов системы, p – количество вычислителей, выполняющих расчет. Эффективной считается загрузка, при которой вычислители завершают расчет дескрипторов одновременно.
Конечной целью расчета каждого вычислителя является получение новых значений элементов одночастичных дескрипторов {Dlv(i)}, рассчитываемых по формуле (1). Для получения новых значений элемента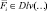 
требуется расчет элементов 
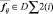, в которых идет пересчет отношений i и j элемента, для всех фиксированных i со всеми j и где i ≠ j
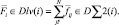(1)
Эта часть расчета имеет квадратную зависимость от числа дескрипторов {Dlv(i)} и является самой затратной по времени в процессе моделирования системы. Сократить время расчета можно за счет уменьшения обсчитываемых отношений между дескрипторами.
Для этого применяется алгоритм «диагональной матрицы», в котором, элемент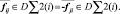 
В этом случае время расчета Dlv{} сокращается в два раза, а количество обсчитываемых отношений становится равным (N(N – 1))/2. На рис. 1 наглядно отображен расчет элементов 
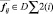, с использованием алгоритма «диагональной матрицы».
В этом случае количество отношений, которые нужно обсчитывать для накопителя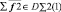 
, равно N – 1, а для 
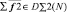, равно 0. Следовательно, если формировать рассчитываемые подмножества дескрипторов {Dlv(i)} для каждого вычислителя последовательными диапазонами с мощностью N/p, то загруженность вычислителей становится не равномерной. Для равномерной загрузки вычислителей разработан встречный алгоритм выборки дескрипторов в диапазон.
Рис. 1. Применение алгоритма «диагональной матрицы» для расчета элементов двухчастичного дескриптора DΣ2(i)
Подмножества одночастичных дескрипторов {Dlv(i)}, рассчитываемых каждым вычислителем формируются по схеме, отображенной на рис. 2.
Все множество дескрипторов разбивается на два интервала [Dlv(i1), Dlv(iN/2)] и [Dlv(iN/2+1), Dlv(iN)][]. В нутрии каждого интервала дескрипторы распределяются по номерам, где i1 – номер первого дескриптора, iN – номер последнего дескриптора. Количество дескрипторов содержащихся в рассчитываемом подмножестве и передаваемых каждому вычислителю равно k. Из номеров дескрипторов находящихся на интервале [Dlv(i1), Dlv(iN/2)] формируется первая половина подмножества, а из номеров интервала [Dlv(iN/2+1), Dlv(iN)] формируется вторая половина подмножества.
Выборка дескрипторов происходит поочередно, сначала из первого интервала начиная с Dlv(i1) затем из второго интервала в обратном направление с Dlv(iN). Каждое подмножество получает следующий дескриптор через шаг равный p. На рис. 2 отображено распределение дескрипторов между вычислителями используя метод равномерной загрузки.
Метод равномерной загрузки вычислителей коррелированной системы N-частиц является оптимальными для однородной вычислительной среды и применяется для параллельного расчета дескрипторов в модели с распределенной памятью. Реализация данного метода в гетерогенной среде, когда совместно используются вычислители разные по типу и производительности, требует доработки. Так как из-за разницы в производительности более мощные вычислители, выполнив свои расчеты, простаивают.
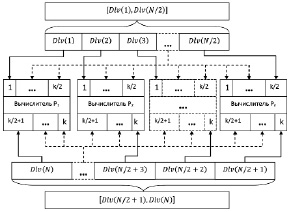
Рис. 2. Формирование подмножеств одночастичных дескрипторов {Dlv(i)} с применением встречного расчета
В настоящее время разработанный метод равномерной загрузки вычислителей для параллельного расчета коррелированной системы N-частиц проходит апробацию в программном комплексе «MD-SLAG-MELT»[8,9].
Библиографическая ссылка
Трунов А.С., Дворянчикова А.А. МЕТОД РАВНОМЕРНОЙ ЗАГРУЗКИ ВЫЧИСЛИТЕЛЕЙ ДЛЯ РАСПРЕДЕЛЕННОГО МД-МОДЕЛИРОВАНИЯ КОРРЕЛИРОВАННОЙ СИСТЕМЫ N-ЧАСТИЦ // Современные наукоемкие технологии. – 2013. – № 6. – С. 116-117;URL: https://top-technologies.ru/ru/article/view?id=32019 (дата обращения: 21.11.2024).