Основной принцип экономической деятельности – максимум эффективности при минимуме затрат ресурсов – предполагает широкое применение математического моделирования в обработке данных, своевременной оценке ситуации, прогнозировании деятельности организации. Математические модели представляют собой основу компьютерного моделирования и обработки информации. Они расширяют наши представления о закономерностях экономических процессов и помогают сформировать мышление и анализ на новом, более высоком уровне.
Понятие производственной функции имеет основополагающее значение в экономической теории. Производственная функция определяет связь между затратами факторов производства и выпуском продукции в производственной системе. Производственная функция описывает наиболее эффективные производственные процессы.
С помощью производственных функций можно оценить эффективность функционирования производственной системы и использования в ней ресурсов, спрогнозировать влияние вносимых изменений и инноваций в производство, выбрать оптимальную стратегию эволюции производственных систем.
Многофакторная производственная функция характеризуется функцией нескольких переменных y = f(x1, x2, ..., xn), где независимые неотрицательные переменные x1, x2, ..., xn обозначают объёмы n используемых ресурсов, а значение функции f(x1, x2, ..., xn) – объём выпуска.
Из производственных функций в микро- и макроэкономике наиболее часто используется двухфакторная производственная функция Кобба-Дугласа. В качестве основных факторов в ней используют капитал, т.е. прошлый (накопленный) труд K в форме остальных производственных фондов и настоящий (живой) труд L, описываемый количеством занятых. Если результатом деятельности экономической системы считается объём выпуска продукции Y, то экономика представляется моделью в форме наиболее распространённой двухфакторной производственной функции Y = F(K, L).
Обычно экономическая система производит несколько различных видов продукции, поэтому объём выпуска удобнее всего исчислять в денежном выражении, например, если в качестве экономической системы рассматривать национальную экономику, то объёмом выпуска можно считать как валовой внутренний продукт, а если в качестве экономической системы рассматривать фирму – то просто выпуск продукции в денежном выражении, т.е. суммарную стоимость производственной продукции всех видов.
Производственная функция называется неоклассической, если она определена при всех неотрицательных значениях аргументов К и L, является непрерывной, дважды дифференцируемой по её аргументам и обладает следующими свойствами:
• F(0, L) = 0 при всех L ≥ 0, F(K, 0) = 0 при всех K ≥ 0, т.е. при отсутствии хотя бы одного из факторов производство невозможно;
• 
, 
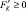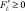, при всех K ≥ 0, L ≥ 0, т. е. при увеличении затрат по одному из факторов выпуск продукции возрастает;
• 
, 
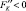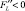для всех K ≥ 0, L ≥ 0, это значит, что при увеличении количества одного из используемых ресурсов при неизменном количестве другого скорость роста выпуска продукции замедляется;
• F(∞, L) = ∞ при всех L > 0, F (K, ∞) = ∞ при всех K > 0, т.е. при неограниченном увеличении количества одного из ресурсов выпуск продукции неограниченно возрастает.
При моделировании макроэкономических процессов часто используется мультипликативная двухфакторная производственная функция Кобба-Дугласа вида Y = Y0∙Kα∙Lβ, где K – объём используемого капитала, L – затраты труда. Выбор значений параметров Y0, α, β определяется статистическими данными за определённый период времени. Согласно статистической обработке экономических данных, проводившейся различными авторами, наблюдаются следующие закономерности: 0 < α < 1, 0 < β < 1, α + β ≈ 1. Нетрудно видеть, что функция Y = Y0∙Kα∙Lβ обладает всеми перечисленными свойствами неоклассических производственных функций.
В таблице приведены значения макроэкономических параметров для стран США и СССР. Коэффициент Y0 положим равным единице.
|
Страна |
Годы |
Параметры |
Вид функции |
|
|
α |
β |
|||
|
США |
1934-1956 |
0,26 |
0,74 |
YСША = K0,26L0,74 |
|
СССР |
1960-1985 |
0,54 |
0,46 |
YСССР = K0,54L0,46 |
Между данными, по которым построены функции, временнóй промежуток – несколько десятилетий. Полагая, что за столь длительное время на первое место выступает технический
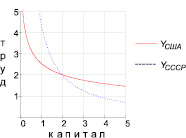
прогресс, проанализируем участие капитала и труда в достижении одинакового объёма производства. Построим на одном графике линии уровня Kα∙Lβ = 2 функций YСША и YСССР (рисунок).
Видно, что за десятилетия линия уровня сдвинулась направо. Это означает, что доля капитала в достижении одинакового объёма производства увеличилась, а доля живого труда уменьшилась. Значит, труд стал более производительным.
Полученная статистическими методами производственная функция позволяет рассчитывать ряд важных характеристик: среднюю и предельную производительности, эластичность по i-му фактору, предельные нормы замены одного фактора другим и т.д. Эти материалы, полученные в аналитическом, графическом и табличном видах, дают возможность экономисту-аналитику проводить исследования экономических показателей производственной деятельности экономического субъекта, начиная от мелкого предпринимателя и заканчивая государством в целом.
Библиографическая ссылка
Сторожева Д.С., Фокина И.А., Ощепкова Ю.С., Агишева Д.К., Матвеева Т.А. МАТЕМАТИЧЕСКИЙ АППАРАТ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ // Современные наукоемкие технологии. – 2013. – № 6. – С. 113-114;URL: https://top-technologies.ru/ru/article/view?id=32016 (дата обращения: 21.11.2024).