Операционное исчисление можно применять для широкого класса кусочно-непрерывных функций f(t) и функцией, заданных графически. Это может быть, например, входной сигнал, действующий на систему автоматического регулирования:
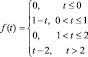
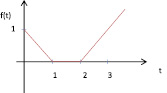
Запишем аналитическое выражение оригинала с помощью единичной ступенчатой функции:
f(t) = (1 – t)(η(t) – η(t – 1) + (t – 2)η(t – 2),
где 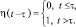
Решим задачу Коши
x″ – 9x = f(x),
где x(0) = 0, x′(0) = 1, где f(t) – функция, рассмотренная выше.
Решение:
1. Перейдем от оригиналов к изображениям:
x(t) = X(p),
x″(t) ↔ p2X(p) – px(0) – x′(0) = p2X(p) – 1.
f(t) можно преобразовать:
f(t) = η(t) − tη(t) + (t − 1)η(t − 1) + (t − 2)η(t − 2).
Тогда, используя теорему запаздывания, изображение этой функции:
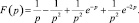
Запишем уравнение для изображений:
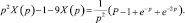
2. Найдем X(p) – изображение решения исходного дифференциального уравнения, удовлетворяющего заданным начальным условиям:
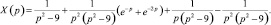
3. По таблице соответствия изображений оригиналам, найдем x(t):
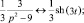
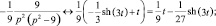
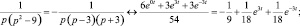
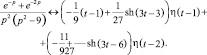
Т.о. решение дифференциального уравнения имеет вид:
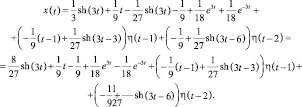
Библиографическая ссылка
Калюжный Д.А., Светличная В.Б. Решение операционным способом дифференциальных уравнений с импульсной правой частью // Современные наукоемкие технологии. – 2013. – № 6. – С. 100-101;URL: https://top-technologies.ru/ru/article/view?id=32005 (дата обращения: 19.04.2024).



