Рамы подразделяются на пространственные и плоские конструкции. Расчет рам обычно производится с помощью общих методов расчета статически неопределимых систем: метод сил, метод перемещений, смешанный метод и в настоящее время – более ускоренный метод приближенного расчета с использованием программного обеспечения на ЭВМ.
Метод сил. Рамы комбинированных почвообрабатывающих машин, шпренгельные устройства, многоопорные брусья и т.п. являются статически неопределимыми системами, в которых имеется больше связей, и число уравнений ,чем это необходимо для равновесия. Для расчета таких конструкций нужно составить дополнительно к уравнениям равновесия недостающее количество уравнений перемещений. Расчет рам носит поверочный характер, так как для расчета нужно знать, или задаться величиной моментов инерции сечений деталей.
Рамные конструкции обычно рассчитывают по методу сил. Избыточные связи в рассчитываемой системе заменяют неизвестными единичными силами и моментами: Х1, Х2, Х3, ..., Хn. Для этого в раме проводят условные разрезы или вставляют условные шарниры так, чтобы получилась статически определимая основная система, нагруженная заданными внешними силами и неизвестными силами и моментами. Величину неизвестных сил и моментов определяют путем совместного решения уравнений перемещений, число которых соответствует числу неизвестных.
Уравнения перемещений имеют вид
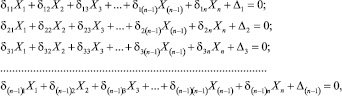
где d11 – коэффициенты, выражающие перемещение в месте приложения силы X = 1 от действия этой силы; d12 = d21 – перемещение в месте приложения силы Х1 (или X2) от действия силы Х2 = 1 = 1 (или Х1 = 1); D1, D2, ... Dn – перемещения в местах приложения сил Х1, Х2, Х3, ..., Хn от действия внешней нагрузки.
Эти уравнения перемещений математически выражают идею, что в рассчитываемой раме линейные или угловые перемещения в местах условных разрезов или шарниров равны нулю. Для подсчета численной величины коэффициентов и свободных членов уравнений перемещений нужно построить для основной системы эпюры моментов от неизвестных сил и моментов от внешней нагрузки. Для этого в сечениях брусьев рамы через центр изгиба (тяжести) проводят оси: продольную и две поперечные (главные центральные оси). Сумма моментов всех сил, действующих по одну сторону сечения, относительно поперечных осей дает величину изгибающих моментов Мизг, расположенных во взаимно-перпендикулярных плоскостях. Сумма моментов всех сил по одну сторону сечения относительно продольной оси дает величину крутящего момента Мкр, действующего в сечении. Коэффициенты уравнений d11, d12, d13, …, dnn подсчитывают путем попарного сопряжения эпюр от единичных сил Х1 = 1, X2 = 1, X3 = 1, ..., Xn = 1. Свободные члены D1, D2, ... Dn подсчитывают путем сопряжения соответствующей эпюры от внешней нагрузки с эпюрами от единичных сил.
Коэффициенты и свободные члены уравнений перемещений подсчитывают или по формуле Мора–Максвелла, или по правилу Верещагина, или с помощью таблиц, в которых приведены эпюры, наиболее часто встречающиеся при расчетах.
Сокращенная формула Мора–Максвелла имеет вид
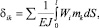
где Мизг – изгибающий момент в каком-либо сечении бруса рамы для состояния i; mk – изгибающий момент в том же сечении для состояния k; EJ – жесткость бруса на этом участке.
Согласно правилу Верещагина, интеграл формулы Мора – Максвелла равен произведению площади одной эпюры моментов на ординату, взятую из второй эпюры (с прямолинейным очертанием) под центром тяжести первой эпюры.
Уравнения перемещений могут быть решены с помощью алгоритма Гаусса, методом детерминантов и т.д. Сущность способа Гаусса заключается в последовательном исключении неизвестных Х1, Х2, Х3, ..., Хn–1. Для этого второе уравнение складывается с первым, умноженным на такой множитель m = d12/d11, чтобы первые члены обоих уравнений в сумме дали нуль. Таким образом, получается второе уравнение алгоритма с меньшим числом неизвестных. В результате нескольких исключений получается последнее уравнение алгоритма с одним неизвестным, которое легко определить. После подстановки найденных значений неизвестных в уравнения алгоритма определяются все неизвестные уравнений перемещений. Изгибающей момент в любом сечении рамы подсчитывают путем суммирования ординат эпюр моментов от единичных сил, умноженных на найденные значения неизвестных, с ординатами эпюры от внешней нагрузки по формуле
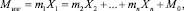
где m1, m1, …, mn – моменты в данном сечении от действия единичных сил; Х1, Х2, ..., Хn – значения неизвестных сил и моментов; М0 – момент в этом же сечении от внешней нагрузки.
После построения суммарной эпюры моментов легко проверить прочность брусьев рассчитываемой рамы.
Рамы начинают разрушаться в местах приложения внешних сил или, что наблюдается чаще, в составных узлах. Напряжения в брусьях рамы, которые легче поддаются расчету, обычно не достигают предельного значения. В узлах рамы, где резко изменяется жесткость отдельных элементов конструкции, всегда наблюдаются пики напряжения, особенно в случае действия крутящих моментов. Очень опасны переменные напряжения в сварных соединениях, где имеет место значительная концентрация напряжений.
Метод узловых моментов. Вычислительная работа может быть уменьшена при расчете плоских рам по методу распределения узловых моментов.
Во время действия внешней нагрузки на раму машины каждый ее узел поворачивается на некоторый угол, пока не наступит упругое равновесие всей рамы. При расчете по методу узловых моментов принимается, что эти повороты узлов происходят не одновременно, а последовательно, т.е. во время поворота одного узла остальные узлы рамы остаются неподвижными. После поворота первого узла последовательно поворачиваются остальные узлы, в результате чего действующие изгибающие моменты от внешних сил распределяются между всеми узлами рамы.
Расчетная схема рамы по этому методу получается путем условной замены всех жестких узлов шарнирами с одновременным введением в них моментных связей, препятствующих относительному повороту концов брусьев. Благодаря такой замене каждый брус рамы превращается в обособленную балку с заделанными концами. Вследствие сопротивления узлов рамы повороту под действием внешней нагрузки в каждом узле возникают реактивные моменты заделки. Узловым моментом называется момент в концевом сечении бруса рамы, действующий на узел. Момент, действующий против часовой стрелки, считается положительным. Узловые моменты от внешней нагрузки можно подсчитать с помощью формул, приведенных в справочниках и специальных таблицах.
Узловые моменты при расчете последовательно распределяются между брусьями рамы пропорционально их удельным жесткостям. Удельная жесткость бруса характеризует его сопротивление деформациям на единицу длины и для бруса постоянного сечения равна отношению осевого момента инерции сечения к длине бруса
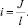
Так как узел рамы состоит из нескольких жестко соединенных брусьев, то каждый брус воспринимает часть узлового момента, определяемую величиной коэффициента распределения. Коэффициент распределения для какого-либо бруса рамы равен отношению удельной жесткости этого бруса к сумме жесткостей всех брусьев, составляющих данный узел, т.е.
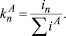
Первоначальное распределение узловых моментов корректируется с учетом взаимодействия всех узлов рамы, связанных в единую жесткую конструкцию. В результате такого взаимодействия на другом конце бруса возникает вторичный узловой момент, величина которого определяется коэффициентом переноса. Для прямых брусьев постоянного сечения коэффициент переноса при изгибе равен
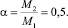
Вторичные узловые моменты складываются в тех узлах рамы, где они действуют совместно, а потом они распределяются, аналогично предыдущему, между стержнями своего узла. Вторичные моменты имеют значительно меньшую величину. Затем распределяются узловые моменты третьего, четвертого порядка и т.д., пока уравновешивающие моменты не уменьшатся настолько, что их величиной можно пренебречь. После нескольких (3–5) циклов распределения вторичных моментов можно подсчитать численную величину моментов, действующих в концевых сечениях брусьев рамы.
Распределение узловых моментов сводится в таблицу. Таблица распределения состоит из нескольких вертикальных колонок и граф. Число колонок таблицы соответствует числу узлов в рассчитываемой раме, число граф в каждой колонке – на единицу больше числа брусьев в данном узле. В заголовке таблицы приводят обозначения узлов, величину коэффициентов распределения и обозначение моментов в концевых сечениях брусьев рамы.
В первой строчке таблицы записывают узловые моменты от внешней нагрузки, которые суммируют в пределах каждого узла и затем распределяют между брусьями данного узла соответственно величине коэффициентов распределения k. Численные значения первичных распределенных моментов записывают во второй строчке таблицы. В третьей строчке в каждой графе таблицы записывают половину узлового момента, действующего на другом конце бруса. Эти вторичные моменты суммируют в пределах каждого узла, затем распределяют между брусьями своего узла, а результаты распределения записывают в четвертой строчке таблицы. В пятой и шестой строчках таблицы записывают узловые и распределенные моменты третьего порядка и т.д.
Величина изгибающего момента в концевом сечении любого бруса рамы получается суммированием составляющих моментов по отдельным графам таблицы распределения. Численные значения моментов в каждой графе представляют собой быстро сходящийся ряд, пределом суммы которого является величина момента, действующего в сечении. Сумма результирующих изгибающих моментов для каждой колонки таблицы должна равняться нулю, т.к. все узлы нагруженной рамы находятся в состоянии упругого равновесия.
Если опоры рамы устроены так, что узлы ее не могут смещаться или если рама и нагрузка симметричны, то расчет плоской рамы по методу распределения узловых моментов выполняется без решения каких-либо уравнений. Если же внеопорные узлы рамы могут смещаться под действием нагрузки, то при расчете необходимо учесть дополнительный изгиб брусьев, вызванный подвижностью узлов. В этом случае рама, в которой жесткие узлы заменены условными шарнирами, является механизмом с одной или несколькими степенями подвижности.
Наличие моментных связей в условных шарнирах обеспечивает только неизменность углов между брусьями рамы, но не может предотвратить бокового смещения внеопорных узлов при нагружении рамы. Для того чтобы предотвратить смещение узлов рамы под действием внешней нагрузки, необходимо условно ввести в раму дополнительные опоры, число которых должно соответствовать степени подвижности полученного условного механизма.
В связи с этим рама при расчете рассматривается в двух состояниях. В первом состоянии на нее действует заданная внешняя нагрузка, вызывающая только поворот узлов. Во втором состоянии внеопорные узлы рамы получают заданные перемещения. Боковые перемещения внеопорных узлов рамы вызывают дополнительный изгиб ее брусьев, вследствие чего возникают новые узловые моменты от перемещений, равные
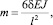
где d – заданное перемещение (например, 1, 10, 100 и т.д.) внеопорного узла рамы; l – длина бруса; EJ – жесткость бруса.
Узловые моменты заделки, вызываемые перемещением узлов, также распределяются между всеми брусьями рамы. По полученным данным можно построить эпюру изгибающих моментов для второго расчетного состояния рамы.
После распределения узловых моментов от нагрузки и перемещений условно вводят в расчетную схему рамы одну или несколько дополнительных опор. От действия внешней нагрузки в дополнительной опоре возникает реакция R, равная сумме составляющих нагрузки и поперечных сил, которые воспринимаются этой опорой. От действия моментов второго расчетного состояния в дополнительной опоре возникает вторая реакция r, препятствующая обратному смещению узлов рамы и равная сумме поперечных сил в сечениях брусьев рамы. Ввиду условности выбора величины перемещения d, опорная реакция r пропорциональна сопротивлению рамы боковому смещению от действия внешней нагрузки. Так как рассчитываемая рама в действительности никакой дополнительной опоры не имеет, то реакция условной опоры, равная сумме реакций первого и второго расчетных состояний, должна быть равна нулю. Поэтому можно составить уравнение
rс + R = 0,
из которого определяется коэффициент пропорциональности с = R/r.
При расчете рамы с учетом подвижности узлов суммарная величина изгибающих моментов в сечениях стержней определяется по формуле
Мизг = М + mс,
где М – момент от действия сил первого расчетного состояния; m – момент от перемещений во втором состоянии; с – коэффициент пропорциональности для сил второго состояния.
Расчет рам на ЭВМ. Если рама состоит из трех и более контуров, то уточнения в расчете, вносимые с учетом подвижности узлов, сравнительно невелики и такую раму комбинированного агрегата можно рассчитывать на действие одной внешней нагрузки. Это позволяет применить при расчете статически неопределимых рам ЭВМ.
Библиографическая ссылка
Анутов Р.М., Котельников В.Я., Козявин А.А., Котельников А.В., Тищенко Д.Е. МЕТОДЫ РАСЧЕТА РАМНЫХ КОНСТРУКЦИЙ КУЛЬТИВАТОРОВ // Современные наукоемкие технологии. – 2013. – № 2. – С. 7-10;URL: https://top-technologies.ru/ru/article/view?id=31321 (дата обращения: 24.04.2024).



