В данной работе изучается метод фиктивных областей одного класса нелинейных начально-краевых задач параболического уравнения. Цель состоит в получении не улучшаемой оценки скорости сходимости.
Итак, в области 
с границей S рассмотрим
начально-краевую задачу для параболического уравнения
(1)
(2)
(3)
Согласно методу фиктивных областей, в области D, строго содержащей в себя область 
, решается уравнения с малым параметром
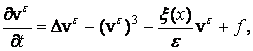(4)
(5)
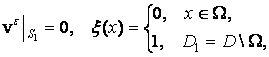(6)
где S1-граница области D.
В предшествующих работах исследована задача (4)-(6). В линейном варианте получена оценка скорости сходимости порядка ε1/4. В настоящей работе предлагается новый способ получения неулучшаемой оценки скорости сходимости по порядку ε для задачи (4)-(6).
Определение.
Обобщенным
решением задачи (4)-(6) называется функция 
, удовлетворяющая интегральному тождеству
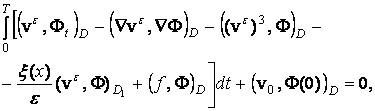(7)
Здесь v0,f - продолжаем нулем вне с сохранением гладкости.
Теорема.
Пусть 
. Тогда существует обобщенное решение задачи (4)-(6) и при ε→0 оно сходится к
обобщенному решению задачи (1)-(3), а также справедлива оценка
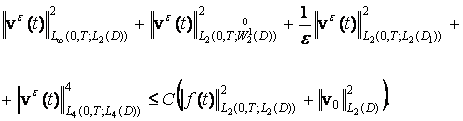(8)
Отсюда следует оценка
. (9)
Итак, получена неулучшаемая оценка скорости сходимости.
Библиографическая ссылка
Куттыкожаева Ш.Н. МЕТОД ФИКТИВНЫХ ОБЛАСТЕЙ ДЛЯ НЕЛИНЕЙНЫХ КРАЕВЫХ ЗАДАЧ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ // Современные наукоемкие технологии. – 2009. – № 10. – С. 45-46;URL: https://top-technologies.ru/ru/article/view?id=25730 (дата обращения: 23.04.2024).