Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова

Бражников А.В. Гилев А.В. Белозеров И.Р. Хомич Л.В.

Приведено описание явления и метода компенсационной фильтрации полигармонических компонент периодических сигналов.

Статья в формате PDF

206 KB

компенсационная фильтрация

явление

метод

При решении ряда технических задач появляется необходимость разделения исходного периодического сигнала на две компоненты, ортогональные по отношению друг к другу в смысле спектрального состава, т.е. когда гармонические составляющие исходного сигнала, входящие в спектр одной его компоненты, отсутствуют в спектре дру­гой. Подобные ситуации возникают, в частности, при создании си­стем передачи информации, устройств и систем безразборной техни­ческой диагностики зубчатых передач [2, 9, 12], гидроакустичес­ких систем и др.

Выделение названных выше компонент исходного периодического сигнала на базе существующих методов связано с предварительным переходом из временной области в спектральную и осуществляется в два этапа:

- выделение (точнее - отфильтровывание) из исходного сигнала гармонических составляющих с заданными частотами;

- синтез искомых компонент исходного сигнала на основе гармонических составляющих, выделенных на первом этапе обработки.

Вследствие этого для осуществления названного выше процесса в настоящее время требуются существенные затраты времени на фильт­рацию отдельных гармоник и синтез искомых компонент сигнала, а также в ряде случаев - значительные затраты аппаратных средств, что является серьезным препятствием при создании устройств и сис­тем оперативного анализа сигналов, обладающих достаточно высокой надежностью и быстродействием.

Для устранения этого препятствия необходима разработка мето­дов, с использованием которых стало бы возможным выделение из периодического сигнала нужных компонент без перехода из временной области на спектральный уровень. Техническая реализация названных методов должна сопровождаться меньшими затратами аппаратуры и времени, необходимых для осуществления процесса фильтрации, чем при использовании существующих методов и технических средств аналогичного назначения.

В качестве одного из решений сформулированной задачи пред­лагается метод, названный авторами этой работы "методом компенсационной фильтрации полигармонических компонент периодических сигналов (МКФ)" [2, 3, 5]. МКФ был разработан авторами данной статьи в результате анализа электромагнитных процессов, происходящих в многофазных системах «автономный инвертор (АИ) - электродвигатель переменного тока (ЭД)», а именно - явления компенсационной фильтрации, возникающего на различных этапах преобразования электромагнитной энергии в названных электромеханических системах. Более подробно это явление рассмотрено ниже.

Базовым элементом МКФ является фильтрующий алго­ритм ФА_m по параметру m, где m - некоторое заданное нату­ральное число; m>1. В соответствии с этим алгоритмом из ис­ходного периодического сигнала f(t) выделяется компонента γ(t) , представляющая собой при разложении в ряд Фурье совокупность всех гармонических составляющих f(t) с угловыми частотами, удовлетворяющими равенству

ω(c_γ)=c_γω                       (1)

где ω - угловая частота основной гармоники исходного сигнала; c_γ - порядок гармоники компоненты γ(t) ;

c_γ=km±n;                          (2)

k=0,1,2,3,...; ; n₀, n_m - некоторые заданные числа;  t- время.

Величина n₀ может принимать значения 0,1,2,3,...,n_m, а n_m - 0,1,2,3,...,n_гр, где

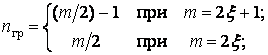
ξ=0,1,2,3,...

Реализация ФА_m заключается в последовательном выполнении следующих процедур. Исходный сигнал f(t) на интервале времени [t_0;(t₀+T)] разделяется на m участков u_i(t), каждый длительностью (рис. 1,а), где T - период f(t); i- номер участка сигнала f(t) ; t₀ - момент начала обра­ботки исходного сигнала. На интервале времени [t₀;t₀+T] величина i принимает значения от 1 до m (т.е. ). Для получения математической модели процесса фильтрации по фильтрующему алгоритму ФА_m, которая будет приведена ниже, целесообразно использовать систему нумерации участков сигнала f(t) , охватывающую два периода f(t) и показанную на рис. 1,б.

На этом рисунке период сигнала f(t) , используемый для выделения компоненты γ(t), отмечен штриховкой. При такой системе нумерации на интервале времени [t₀;t₀+T] величина i принимает значения от (1-m) до m, т.е. . В этом случае вследствие периодичности f(t) выполняется ра­венство u_e(t)=u_j(t), где e=j-m.

Для выделения компоненты γ(t) сигнала f(t) необходимо и достаточно обработать f(t) на интервале времени, дли­тельность которого равна периоду исходного сигнала, т.е. сигнала f(t) . При этом формирование γ(t) осуществляется отдельно на каждом из m интервалов времени дли­тельностью , где . Причем на интервале θ_p образу­ется p-й участок γ_p(t) составляющей γ(t) , а совокупность γ_p(t) на интервале времени [t₀;t₀+T] представ­ляет собой искомую компоненту γ(t) сигнала f(t) , то есть 

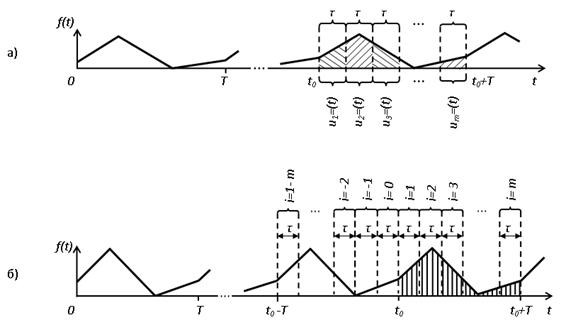
Рис. 1. Выделение участков исходного сигнала и система их нумерации: а - выделение участков исходного сигнала; б - система нумерации участков исходного сигнала

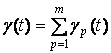.                                                      (3)

Каждый участок γ_p(t) формируется путем сложения u_i(t), предварительно умноженных на соответствующие масштабные коэффициенты:

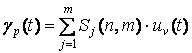,                                              (4)

где

;                                                          (5)

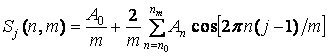.                       (6)

Коэффициенты A₀ и Am (при всех ) могут при­нимать значения либо 0, либо 1 , которые выбираются исходя из требований, предъявляемых к спектральному составу компоненты γ(t) . Методика выбора значений этих коэффициентов будет приведена ниже.

Все гармонические составляющие исходного сигнала f(t) , порядки которых не удовлетворяют равенству (2), взаимно уничтожаются в результате выполнения операции сложения, представленной в (4). Наличие такого эффекта побудило авторов этой работы назвать описываемый здесь метод "методом компенсационной фильтрации".

Из вышеизложенного следует, что для использования предлагаемого метода фильтрации необходимо априори (до начала соответствующего процесса обработки сигнала) знать длительность периода исходного сигнала.

Для получения математической модели описанного процесса фильтрации целесообразно представить этот процесс повторяющимся с периодом, равным T, а также воспользоваться спектрально-гармони­ческим представлением периодически изменяющихся величин.

Любой исходный периодический сигнал f(t) может быть представлен в виде ряда Фурье:

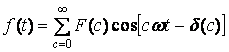,                                    (7)

где c - порядок гармоники сигнала f(t) ; F(c) и σ(c) - со­ответственно амплитуда и фаза c-й гармоники f(t) ; .

Разделению каждого периода сигнала f(t) на m участков длительностью соответствует умножение f(t) на систему избирательных функций E_i(t), которые определяются по следующей формуле:

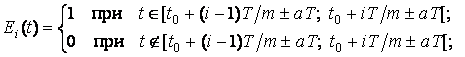             (8)

где ; a=0,1,2,3,...

При этом в результате умножения f(t) на функцию E_i(t) происходит выделение из f(t) участка u_i(t) этого сигнала.

Избирательные функции E_i(t), описывающиеся выражением (8), могут быть разложены в ряд Фурье:

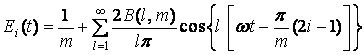,              (9)

где l - порядок гармоники функции E_i(t);

.

С учетом (7) и (9), выражение, описывающее участок u_i(t) сигнала f(t) , будет иметь вид

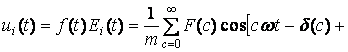
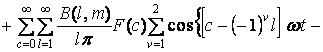
.                                          (10)

Для получения математического описания участка γ_p(t) компоненты γ(t) исходного сигнала f(t) необходимо сместить все выделенные участки u_i(t) на временной интервал . На основании (10) выражение для i-го смещенного участка u_i(t) можно записать следующим образом:

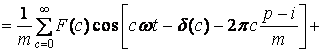
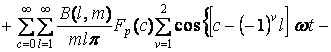
                           (11)

С учетом введенного понятия "смещенный учсток исходного сигнала" выражение (4) для участка γ_p(t) компоненты γ(t) преобразуется к виду

.

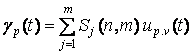Последнее выражение с учетом (5), (6) и (11) можно предста­вить следующим образом:

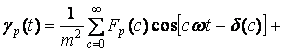
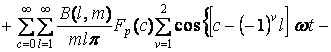
,                                        (12)

где

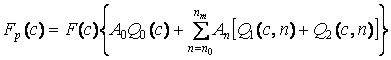;       (13)

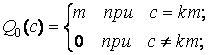                                          (14)

                               (15)

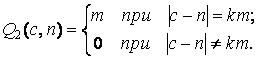                               (16)

В результате подстановки (12) в (3) и определения суммы по p, а также с учетом (13)-(16) может быть получено следующее выражение для компоненты γ(t) исходного сигнала f(t) :

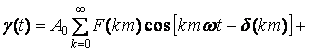
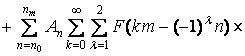
.                         (17)

Анализ выражения (17) показывает, что в спектре компоненты γ(t) присутствуют только гармонические составляющие исходного сигна­ла f(t) , угловые частоты которых при A₀,A_n=1 для всех удовлетворяют равенству (1). Указанные составляющие имеют те же амплитуды и фазы, что и соответствующие гармоники сигнала f(t) .

Как отмечалось выше, значения коэффициентов A₀ и A_n (при ) выбираются исходя из требований, предъявляемых к спектральному составу компоненты γ(t) исходного сигнала f(t) . В том случае, если в спектре γ(t) должны присутствовать гармони­ческие составляющие f(t) с порядками c_γ=km, то значение A₀ принимаетcя равным 1, в противном случае A₀=0. Аналогич­но производится выбор значений A_n: если в спектральный состав компоненты γ(t) должны войти гармоники f(t) с порядками c_γ=km±n_k (где n_k - некоторое значение n; n₀≤n_k≤n_m), то

если - нет, то выбирается

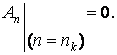
Таким образом, значения коэффициентов A₀ и An определяют фильтрующие свойства алгоритма ФА_m. Поэтому в дальнейшем A₀ и A_n будут име­новаться "коэффициентами фильтрации".

В том случае, когда компонента γ(t) при разложении в спектр должна представлять собой совокупность только тех гармони­ческих составляющих исходного сигнала f(t) , порядки которых удовлетво­ряют равенству c_γ=km (т.е. когда A₀=1, а A_n=0 при всех ), формирование одного периода γ(t) достаточно производить на интервале времени длительностью с дальнейшим повторением полученного сигнала на последующих интер­валах времени такой же длительности. Это обусловлено тем, что в рассматриваемом случае период γ(t) равен . Однако для получения другого спектрального состава компоненты γ(t) такая организация процедур ФА_m неприемлема.

Параллельная или последовательная (во времени) обработка исходного сигнала f(t) по конечному множеству фильтрующих алгоритмов ФА_m с различными сочетаниями значений параметра m и коэффициентов фильтрации позволяет сформировать практически любой спектральный состав компоненты γ(t) .

Выше уже указывалось на то, что при использовании ФА_m параметры гармонических составляющих (амплитуды, фазы), входящих в спектр γ(t) имеют те же значения, что и соответствующие гармоники исходного сигнала. Вследствие этого при вычитании γ(t) из f(t) образуется компонента h(t) сигнала f(t) , ортогональная компоненте γ(t) в смысле спектрального состава. При разложении в ряд Фурье h(t) представляет собой сово­купность только тех гармонических составляющих f(t) , которые отсутствуют в спектре γ(t).

Реализация МКФ возможна на базе как стандартных, так и специальных цифровых устройств. Эти устройства и прог­раммное обеспечение МКФ проще, а затраты времени на обработку исходного сигнала с применением МКФ меньше, чем при использовании других существующих методов аналогичного назначения, особенно в том случае, если МКФ применяется в комплексе с известными методами определения параметров гармонических сигналов за время меньше периода (например, [10, 11]).

Как отмечалось выше, основные положения МКФ были сформулированы авторами данной статьи в результате анализа электромагнитных процессов, происходящих в многофазных системах АИ-ЭД. А именно - явления компенсационной фильтрации (ЯКФ), возникающего на различных этапах преобразования электромагнитной энергии, которое происходит в процессе работы указанных электромеханических систем.

Математически обобщенное ЯКФ может быть сведено к линейному преобразованию, связанному с определением сумм вида

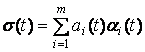,                                             (18)

где a_i(t) - некоторая периодическая функция (в общем случае - несинусоидальная), которая может быть представлена в виде следующего гармонического ряда:

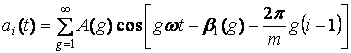;                 (19)

g - порядок (номер) гармоники функции a_i(t); A(g) и B₁(g) - соответственно амплитуда и фаза g-й гармоники a_i(t); ω₁ - угловая частота основной (первой) гармоники функции a_i(t); ; α_i(t) - оператор линейного преобразования;

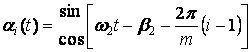                              (20)

ω₂ и β₂ - соответственно угловая частота и начальная фаза функции α_i(t).

Выражение (18) с учетом (19) и (20) принимает вид

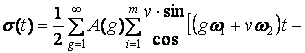
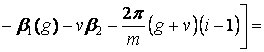
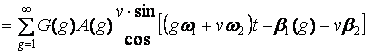,             (21)

где

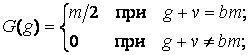                                (22)

; .

Как показывает совместный анализ выражений (21) и (22), в спектре функции σ(t) будут присутствовать только гармоники порядков g=bm±1. Гармоники порядков g≠bm±1 в процессе линейного преобразования (18) взаимно уничтожаются (компенсируются). Именно на этом эффекте основывается МКФ.

Подробное описание (в том числе и математическое) электромагнитных процессов и ЯКФ, наблюдающихся в многофазных системах АИ-ЭД, приведено, в частности, в [1, 4].

Таким образом, использование МКФ позволяет во временной области (без перехода на спектральный уровень) выделять из исходного периодического сигнала два ортогональные в смысле спектрального состава компонента, спектральные составы которых мо­гут быть сформированы практически любыми. Процедуры фильтрации на базе предложенного метода достаточно просты, что обуславливает сравнительно малое время обработки исходного сигнала и относительную простоту аппаратных и программных средств, на основе которых производится реализация МКФ.

Детальное изучение ЯКФ позволило авторам данной статьи не только разработать МКФ (для области анализа сигналов), но и получить ряд важных результатов в области электромеханических систем переменного тока. В частности, на основе анализа ЯКФ были сформулированы принципы построения новых поколений магнитогидродинамических систем принудительной циркуляции металлических расплавов и инверторных электроприводов переменного тока с расширенными регулировочными возможностями [6-8].

СПИСОК ЛИТЕРАТУРЫ

1. Бражников А.В. Многофазный инверторный электропривод с различным исполнением ротора асинхронного двигателя // Диссертация канд. техн. наук, защищена 26.06.1985 г., № ГР 01830052658. - Красноярск, 1985. - 210 с.

2. Бражников А.В. Компенсационные методы обработки виброакустических сигналов редукторов // Сборник научных трудов «Молодые ученые - КАТЭКу». - Красноярск: Издательство КАТЭКНИИуголь, 1988. - С. 28-30.

3. Бражников А.В., Кочетков В.П. Метод компенсационной фильтрации компонент периодических сигналов // Депонированная рукопись. - ЦНИИТЭИприборостроения. - №5027-пр91, 1991. - 11 с.

4. Кочетков В.П., Бражников А.В., Дубровский И.Л. Теория электропривода. - Красноярск: Издательство КрПИ, 1991. - 140 с.

5. Бражников А.В. и др. Общая характеристика работ по созданию теории компенсационных модулированных фильтрующих систем // Сборник материалов Всероссийской научной конференции «Молодежь и наука - третье тысячелетие». - Красноярск: Издательство КРО НС «Интеграция», II часть, 2006. -
С. 295-302.

6. Бражников А.В., Гилев А.В., Довженко Н.Н., Белозеров И.Р. Разработка и создание нового поколения магнитогидродинамических систем принудительной циркуляции металлических расплавов // Современные наукоемкие технологии. - № 1, 2009. - С. 8-9.

7. Бражников А.В., Гилев А.В., Довженко Н.Н., Белозеров И.Р. Разработка и создание нового поколения инверторных электроприводов переменного тока с расширенными регулировочными возможностями // Фундаментальные исследования. - № 2, 2009. - С. 72-73.

8. Бражников А.В., Гилев А.В., Белозеров И.Р. Нетрадиционный способ регулирования скорости многофазного асинхронного электродвигателя // Фундаментальные исследования. - № 5 (приложение), 2009. - С. 10-12.

9. Генкин М.Д., Соколова Л.Г. Виброакустическая диагностика машин и механизмов. - М.: Машиностроение, 1987. - 288 с.

10. Левин М.И., Семко Ю.И. Определение параметров периодических сигналов путем измерения их мгновенных значений // Автометрия. - № 1, 1966. - С. 33-40.

11. Угольков В.Н., Мешков В.П. Методы измерения амплитуды гармонического сигнала за время менее периода // Метрология. - № 8, 1984. - С. 8-11.

12. Наrting D.R. Demodulated Resonance Analysis - A Powerful Incipient Failure Detection Technique. - ISA Transactions, 1977, vol. 17, №1, pp. 35-40.

Библиографическая ссылка