В общем случае пятно контакта недеформируемого инструмента с пластичной поверхностьюпредставляютсобойпространственную фигуру,образованнуюнаинструменте(торе,цилиндре,шаре)пересечением пластичнойповерхностидетали-чаще всего цилиндра. Поэтому для нахождения площади пятнаконтактанеобходиморешатьзадачуопересечениидвухпространственных фигур. При электромеханической обработке наиболее частоприменяетсяинструмент, рабочая поверхностькоторого представляет собой поверхность тора.При обработке деталей типа втулок обрабатываемая поверхность представляет собой цилиндр.
Исходя из вышесказанного,считаем,что наиболее общим случаем контакта инструмента с деталью является задача о пересечениицилиндра с тором. Пятно контакта являетсячастьюповерхности жесткого тора, ограниченнойпересечением с пластичным цилиндром.
Рассмотрим поверхность контакта цилиндра и ролика в виде тора по внутренней поверхностицилиндра.
Уравнение поверхности тора, внедряемойвцилиндр, в декартовой системе координат запишется:
Раскрываяскобкуивозводявквадрат,получим:
Длявычисленияповерхностинеобходимонайтичастныепроизводные
и 
:
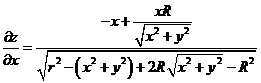
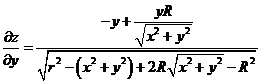
Переходякцилиндрическойсистемекоординат вычисляемплощадьповерхностипоформуле
.
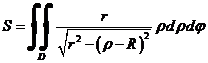ДлявычислениянеобходимонайтипределыинтегрированияпообластиDприпереходекдвукратномуинтегралу.
Рассмотримрисунок1.Уравнениеокружности сеченияцилиндра в декартовойсистемекоординат запишется:
,
где a-координатацентра окружности по оси Ox ; b -радиусокружности. Раскроемскобкииприпомощи формул 
перейдемкполярнойсистемекоординат: .
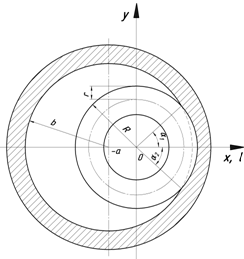
Рис. 1. Расчетнаясхемадляопределенияплощадипятнаконтакта
Уравнение окружности сечения цилиндра в полярной системе координат:
.
Областьинтегрированияограниченас однойстороныуравнениемокружностивнутри сеченияцилиндра, ас другойстороныуравнениемвнешнейокружноститора 
,тогда вполярнойсистемекоординат площадьповерхности пятна вычисляетсяпоформуле:
.
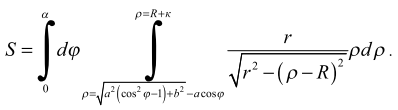Площадьпятнаконтактаопределяетсякаксуммаплощадейконтактавзонахпластическойиупругойдеформации.
Сначаланайдемплощадьпятнаконтактавзонепластическойдеформациипризаданныхзначенияхразмероввалаиролика(в мм).
r =3, R =30 , a = 7,4, b = 40,
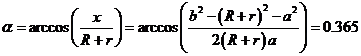
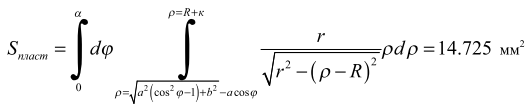
Затем найдемплощадьпятнаконтактавзоне упругойдеформацииприb =40,2:
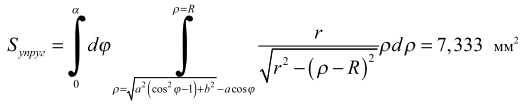
Общая площадь пятна контакта S = Sпласт + Sупруг = 22,058 мм2
Библиографическая ссылка
Гришин О.П., Настин А.А., Исаев Ю.М., Морозов А.В. ОПРЕДЕЛЕНИЕ ПЯТНА КОНТАКТА ИНСТРУМЕНТА С ДЕТАЛЬЮ // Современные наукоемкие технологии. – 2007. – № 4. – С. 55-57;URL: https://top-technologies.ru/ru/article/view?id=24864 (дата обращения: 19.04.2024).