В любом случае суть сегментации состоит в устойчивом разделении покупателей по какому-либо признаку на две или несколько групп и установлении для каждой из них своих цен. При этом весьма актуальной представляется задача оптимального ценообразования на каждом сегменте, а также определения их долей в общем объеме рынка сбыта, обеспечивающих торговой организации максимальную прибыль.
Математическому описанию этого процесса посвящен ряд работ. В частности, в [2] получено следующее соотношение для оптимальных цен на двух сегментах рынка:
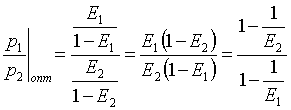 (1)
(1)
При этом авторы данной работы исходили из принципа равенства предельных доходов продавца на каждом сегменте и в качестве основной количственной характеристики данного сегмента, принципиально отличающей его от других, выбрана эластичность спроса по цене, ведь именно этот показатель наиболее полно описывает совокупные свойства того или иного сегмента рынка конечных потребителей.
В предлагаемой работе рассматривается моделирование процесса сегментации рынка сбыта с точки зрения математического программирования. Такой подход представ-ляется авторам весьма перспективным, позво-ляющим решать разнообразные экономико-математические задачи в самой общей постановке, исходя «из первых принципов», с использованием средств вычислительной техники.
Задача решалась в следующей формулировке.
Торговое предприятие занимается реали-зацией однородного товара. Общий объем реализации равен Q. Объемы продаж по сегментам равны Q1, Q2,... Qn соответственно. Тогда 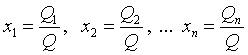 - доли сегментов в общем объеме рынка. Розничные цены по каждому сегменту рынка обозначены через p1, p2 ,...pn..
- доли сегментов в общем объеме рынка. Розничные цены по каждому сегменту рынка обозначены через p1, p2 ,...pn..
В качестве аналитической зависимости объема продаж на данном сегменте от цены используется функция постоянной эластичности
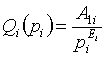 (2)
(2)
где Ei-эластичность спроса по цене на i-ом сегменте.
Выбор зависимости (1) обусловлен следующимим причинами.
Во-первых, это простой и одновременно самый общий вид зависимости спроса от цены товара, дающий хорошее приближение для практических расчетов.
Во-вторых, коэффициенты уравнения (2) имеют прозрачный экономический смысл: Ei показывает, на сколько процентов уменьшается спрос на i-ом сегменте при повышении цены реализуемого товара на 1%; параметр Аi может быть истолкован как объем продаж на i-ом сегменте при единичной цене.
В-третьих, параметры функции (1) могут быть легко определены на основе фактической информации с использованием аппарата корреляционно-регрессионного анализа, в частности, метода наименьших квадратов.
Кроме того, определение ценовой эластичности спроса, т.е. его чувствительности к изменению рыночной цены, является, по мнению авторов, одной из основных целей всего комплекса маркетинговых исследований.
Целью задачи является определение оптимальных цен на каждом сегменте рынка, обеспечивающих максимальный общий доход продавца R. В результате приходим к следующей задаче нелинейного программирования:
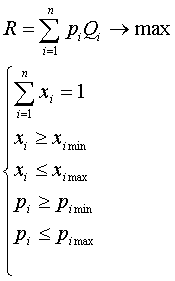 (3)
(3)
Здесь x i min, x i max -минимальная и максимальная доли i-го сегмента в общем объеме рынка;p i min, p i max -минимально возможная и максимально возможная цены для i-го сегмента рынка. Эти параметры несколько субъективны, однако, по мнению авторов, позволяют более гибко учитывать рыночную конъюнктуру.
Оптимизационная задача (3) решалась численно с помощью надстройки «Поиск решения» табличного процессора Microsoft Excel 97 по встроенному алгоритму нелинейной оптимизации Generalized Reduced Gradient (GRG2), разработанному Леоном Ласдоном (Leon Lasdon, University of Texas at Austin) и Аланом Уореном (Allan Waren, Cleveland State University).
Некоторые результаты численных расчетов приведены на рис. 1-3. Для удобства графического представления и анализа полученных результатов авторы ограничились случаем двух сегментов.
При построении графиков использовались следующие условные значения параметров модели: А1=А2=5000р., x1min=x2min=0%, x1max= =x2max=100% , p1min= p2min=0,01 р. , p1max= p2max=3,00 р. На всех графиках E1=2, значение E2 отложено по горизонтальной оси.

Рисунок 1. Зависимость оптимальных цен по отдельным сегментам от Е2. при Е1=2. 1-p1 , 2-p2

Рисунок 2. Зависимость доходов по сегментам R1 , R2, а также общего дохода R от от Е2. при Е1=2.
1- R1, 2- R2, 3- R

Рисунок 3. Зависимость долей сегментов в общем объеме рынка от Е2 при Е1=2. 1-x1 , 2-x2
Для случая двух сегментов авторами получено также аналитическое описание поставленной задачи. С учетом (2) задача сводится к нахождению максимума функции дохода
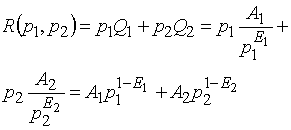 (4)
(4)
при ограничениях
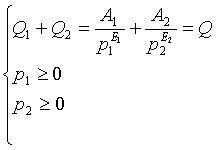 (5)
(5)
В результате получаем задачу на нахождение условного максимума функции двух переменных (4) с дополнительными условиями (5).
Решение ее методом неопределенных множителей Лагранжа [2] приводит к искомому соотношению между ценами на сегментах, максимизирующему доход продавца:
 (6)
(6)
Следует отметить, что (6) полностью совпадает с (1), хотя и получено с использованием другого подхода к рассматриваемой проблеме.
Соотношения (1) и (6) имеют смысл только при выполнении условия E1 ≥ 1, E2 ≥ 1 , т.е. в случае эластичного спроса на обоих сегментах. Однако этот факт нисколько не умаляет ценность полученных результатов, поскольку реальный спрос на подавляющее большинство товаров при равновесной цене эластичен, так как в противном случае происходил бы неограниченный рост цены на неэластичных сегментах, что противоречит действительности.
Результаты проведенного анализа позволяют, прежде всего, сделать практически важный вывод о том, что сегментация рынков сбыта всегда выгодна для продавца. Это следует из того факта, что общий доход продавца минимален при E1= E2 , что на практике означает слияние двух сегментов рынка в один, т.е. отсутствие сегментации (рис.2).
Анализ рис.3. свидетельствует о том, что при эластичном спросе (Ei>1) доля сегмента в общем объеме рынка с ростом эластичности монотонно возрастает; для неэластичных сегментов (Ei<1) наблюдается обратная закономерность.
Кроме того, на менее эластичных сегментах продавец может устанавливать более высокие цены (рис.2), что вполне объяснимо с экономической точки зрения, поскольку на таких сегментах спрос более устойчив.
В целом анализ полученных результатов указывает на адекватность построенной экономико-математической модели и применимость методов математического программирования к решению широкого спектра практических задач, связанных с оптимизацией поведения предприятия в условиях рыночной экономики.
Список литературы
- Герасименко В.В. Целевая политика фирмы. - М.: Финстат -информ, 1995
- Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник.- М.: МГУ им. М.В. Ломоносова, Издательство «ДИС», 1998. - 368 с.
- Котлер Ф. Основы маркетинга: Пер. с англ. / Общ. ред. и вступ. ст. Е.М. Пеньковой - М.: Прогресс, 1996 - 736 с.
Библиографическая ссылка
Копылов А.В., Просвиров А.Э. ПРОБЛЕМА ОПТИМАЛЬНОГО ЦЕНООБРАЗОВАНИЯ НА СЕГМЕНТИРОВАННОМ РЫНКЕ КАК ЗАДАЧА МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ // Современные наукоемкие технологии. – 2004. – № 2. – С. 33-36;URL: https://top-technologies.ru/ru/article/view?id=21610 (дата обращения: 19.04.2024).



