Дистрибутивным асинхронным автоматом называется пятерка (S, s0, E, I, Tran), состоящая из множеств S и E, элемента s0 ∈ S, отношения Tran ⊆ S×E×S и семейства антирефлексивных симметричных отношений I ⊆ (Is)s ∈ S, Is ⊆ E×E. Должны быть выполнены следующие условия:
i Если (s, a, s′) ∈ Tran и (s, a, s″) ∈ Tran, то s′ = s″
ii Для любых
s ∈ S, (a1, a2) ∈ Is, (s, a1, s1) ∈ Tran, (s1, a2, s′) ∈ Tran,
существует такое s2 ∈ S, что (s, a2, s2) ∈ Tran и (s2, a2, s′) ∈ Tran (см. рисунок).
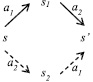
Аксиома (ii) для дистрибутивных асинхронных автоматов
Всякую асинхронную систему (S, s0, E, I, Tran) можно рассматривать как дистрибутивный асинхронный автомат, полагая Is = I для всех s ∈ S.
Определим сеть Петри как пятерку (P, T, pre, post, M0), состоящую из конечных множеств P и T, функций M0:P → N, pre: T → NP, post: T → NP . Здесь NP обозначает множество всех функций P → N. Элементы p ∈ P называются местами, t ∈ T – переходами, M ∈ NP – маркировками, а M0 – начальной маркировкой. Определим отношение порядка на NP, полагая M ≤ M′, если для всех p ∈ P верно M(p) ≤ M′(p). Сумму и разность функций определим как (M ± M′)(p) = M(p) ± M′(p). Для M, M′ ∈ NP и t ∈ T запись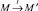 
будет означать, что выполнены условия M ≥ pre(t) и M′ = M – pre(t) + post(t) . В этом случае будем говорить, что маркировка M′ получена из M с помощью срабатывания перехода t.
Пусть (P, T, pre, post, M0) – сеть Петри. Обозначим t = {p ∈ P: pre(t)(p) ≠ 0}. Сеть Петри (P, T, pre, post, M0) определяет дистрибутивный асинхронный автомат (S, s0, E, I, Tran), S = NP, E = T, s0 = M0, Tran = {(M, t, M′) ∈ NP×T×NP существует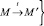 
, для которого Im = {(t1, t2) ∈ T×T:M ≥ pre(t1) и t1 ∩ t2 = ∅}.
Временная сеть Петри это кортеж (N, eft, lft), где N – сеть Петри, eft: T → N, lft: T → N – функции, описывающие соответственно раннее и позднее время доступности переходов, которые удовлетворяют ограничению eft(t) ≤ lft(t) для каждого t ∈ T. Обобщим определение временной сети Петри. Обозначим через R≥0 множество всех неотрицательных вещественных чисел. Временным дистрибутивным асинхронным автоматом (A, eft, lft) называется дистрибутивный асинхронный автомат A = (S, s0, E, I, Tran) вместе с парой функций eft: E → R≥0, lft: E → R≥0 ∪ {∞}, удовлетворяющих для всех a ∈ E неравенству eft(a) ≤ lft(a).
Введем временные состояния. Определим отображение S×E → S⊔{*}, полагая s∙a = s′, если (s, a, s′) ∈ Tran. Если таких s′ ∈ S не существует, то положим s∙a = *. Временным состоянием временного дистрибутивного асинхронного автомата (A, eft, lft) называется пара (s, h) , состоящая из s′ ∈ мS и функции h: E → R≥0 ∪ {#}, таких что s∙a ∈ S ⇒ h(a) ≤ lft(a) и s∙a = * ⇒ h(a) = #. Каждое действие a ∈ E имеет «часы». В начале работы временное состояние равно (s0, h0), где h0(a) = 0, если существует s′ ∈ S и переход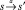 
.
Рассмотрим асинхронную систему, состоящую из двух независимых действий a1 и a2 и четырех состояний
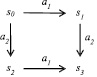
для которых известные ft(ai) и lft(ai), i ∈ {1, 2}. Вычислим минимальное время выполнения операций, приводящих к состоянию s3. Временные состояния (s, h) будем рассматривать как тройки (si, τ1, τ2). Пусть eft(a1) ≤ eft(a2). Тогда возможен следующий путь выполнения:
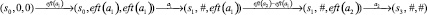
Легко видеть, что полученное время, равное сумме eft(a1) + eft(a2) – eft(a1) будет минимальным. Следовательно, в общем случае минимальное время будет равно max (eft(a1), eft(a2)). Аналогично получим, что максимальное время выполнения действий будет равно max (lft(a1), lft(a2)).