Широко распространенным видом механических передач являются винтовые механизмы (типа винт-гайка). Данные механизмы отличаются простотой конструкции и высокой надежностью, большим передаточным отношением и высокой точностью параметров выходного движения. Они компактны и хорошо компонуются с другими узлами и деталями в различных установках. Развитие современной техники привело к созданию ряда винтовых механизмов, различающихся не только конструктивным исполнением и технико-эксплуатационными характеристиками, но, в ряде случаев, и принципом преобразования вращательного движения в поступательное.
Все винтовые механизмы обычно подразделяют на кинематические, используемые в малонагруженных приводах приборов и систем управления, и силовые, работающие при значительных нагрузках на ходовой винт. К кинематическим передачам винт-гайка предъявляются высокие требования по точности, а к силовым – по прочности и износостойкости.
Развитие современной техники потребовало создания таких винтовых механизмов, которые удовлетворяют всему комплексу требований, предъявляемых как к кинематическим, так и к силовым механизмам [1, 2].
В настоящее время все более широкое применение находят несоосные винтовые механизмы (НВМ), к которым относятся и планетарные передачи винт-гайка качения с резьбовыми роликами (РВП). Детали НВМ имеют несущие винтовые поверхности специального профиля, к которым предъявляются высокие требования по геометрической точности, контактной жесткости, усталостной прочности и долговечности.
Расчет основных конструктивных размеров НВМ производится на основании расчетов деталей на нагрузочную способность, определяемую для НВМ прочностью по критериям контактной и изгибной выносливости, износостойкости. Существующие методики расчета заимствованы из теории зубчатых передач, что не позволяет учесть важные особенности контактного взаимодействия сопрягаемых деталей НВМ.
Одной из актуальных проблем современного машиностроения является проблема повышения долговечности элементов машин по критериям прочности при одновременном снижении их металлоемкости. Непрерывное увеличение мощностей, скоростей, грузоподъемности и других параметров машин и связанный с этим рост напряженности элементов приводят к тому, что указанную проблему можно решить лишь при использовании в процессе конструирования и расчета новейших достижений науки о прочности. По мере развития методов расчета на прочность при одновременном снижении запасов прочности и материалоемкости деталей машин и конструкций традиционные инженерные расчеты по напряжениям (преимущественно номинальным) необходимо дополнять или заменять расчетами по энергетическим критериям прочности.
Известно, что расчет основных конструктивных размеров НВМ необходимо назначать исходя из расчетов деталей на нагрузочную способность, определяемую для НВМ прочностью по критериям контактной, в том числе глубинной, и изгибной выносливости, износостойкости [3, 4]. Существующие методики расчета заимствованы из теории зубчатых передач и подшипников качения, что не позволяет учесть важные особенности контактного взаимодействия сопрягаемых деталей НВМ, имеющего фрикционный характер.
По мере расширения области применения винтовых передач ужесточаются требования к снижению их массы, габаритных размеров, повышению КПД, надежности и долговечности. В обеспечении этих требований (наряду с качеством изготовления, выбором оптимальных расчетных схем, материалов, термообработки) решающая роль принадлежит совершенствованию методов расчета напряженного состояния винтовых поверхностей сопрягаемых деталей.
Напряженное состояние в сечении витка
Напряженное состояние в сечении витка формируется в результате взаимодействия контактных напряжений, напряжений винта и витка. Под напряжениями витка подразумеваются напряжения, вызванные деформациями изгиба, сдвига, растяжения-сжатия, кручения витка резьбы [5].
Важнейшей задачей инженерного расчета является оценка прочности деталей по известному напряженному состоянию, т.е. по известным главным напряжениям в точках тела. Так как в данном случае опасное (предельное) состояние нагруженного тела определяется предельной величиной накопленной удельной энергии формоизменения, то условие прочности будет иметь вид
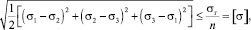
где σт – предел текучести материала; n – коэффициент запаса прочности; [σ] – допускаемое напряжение.
Выбор коэффициента запаса прочности n, показывающего во сколько раз допускаемое напряжения меньше опасного, зависит от состояния материала (хрупкое, пластичное), характера приложения нагрузки (статическая, динамическая, повторно-переменная), а также от таких общих факторов, как неоднородность материала, неточность в задании внешних нагрузок, приближенность расчетных схем и формул и т.п.
При анализе напряжений действующих в деталях, следует принимать во внимание остаточные напряжения, возникшие при изготовлении. Если детали работают в области упругих деформаций, то остаточные напряжения можно учитывать сложением их с напряжениями от рабочих нагрузок [6].
Напряженно-деформированное состояние витков зубьев винтовых и зубчатых передач характеризуется большой интенсивностью напряжений в сравнительно небольших объемах элементов, резкой концентрацией напряжений и деформаций в зоне контакта витков и у их оснований.
Поверхности витков имеют сложную геометрию. В разных зонах (в частности, в разных торцовых сечениях) по длине зуба или витка различны не только максимальные напряжения, но в общем случае и законы распределения напряжений по времени при переменных нагрузках. Различен может быть также объем наиболее напряженного материала. Определение напряжений в витках несоосного винтового механизма (НВМ) является сложной пространственной задачей.
Виток детали НВМ развернутый на плоскость рассчитывается с использованием расчетной модели консольной балки переменного сечения [7]. Аналогичная расчетная модель была использована при определении изгибной деформации зуба и витка червяка и зуба червячного колеса глобоидной передачи. Напряжения в них определяются только от изгибающего момента и в редких случаях от перерезывающей силы. В данном исследовании учитываются все виды деформаций витка.
Виток в процессе эксплуатации испытывает деформации изгиба от сил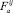 
, 
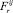, деформации растяжения (сжатия) от силы 
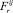, деформации среза от сил 
, 
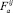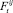и деформацию кручения от силы . Знаки напряжений изменяются в зависимости от направления сил 
, 
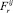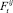и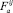 
. Первый индекс i указывает сколько сил действует на виток, второй j – номер витка. В области витка имеем объемное напряженное состояние.
В целях приведения уравнения расчета эквивалентных напряжений к более простому виду и анализу полученного решения производился переход в формулах напряжений к безразмерным коэффициентам. Величина радиальной и тангенциальной составляющих сил давления и трения выбиралась максимальной для конкретных геометрических параметров винтовой поверхности [8].
Осуществлялся переход к безразмерной системе координат. Оценивалась величина относительно эквивалентного напряжения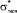 
, характеризующего отношение действующего в элементарном объеме эквивалентного напряжения σэкв к напряжению, сформированному под влиянием суммарной осевой нагрузки Fа и равному 
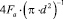. Выбор базы для сравнения основан на том, что именно по осевой нагрузке производится проектный расчет НВМ на прочность.
Заключение
В результате расчетов определялись значения относительных эквивалентных напряжений в 2850 точках факторного пространства. Данные численного эксперимента обрабатывались с целью получения регрессионной модели, отражающей зависимость эквивалентного напряжения от: геометрических параметров витка – угла профиля и угла подъема резьбы; высоты витка; величины смещения точки контакта по высоте витка; силы (коэффициента) трения [9]. Учитывалось смещение точки контакта со среднего диаметра только по направлению к вершине витка.
В результате исследований разработана следующая математическая модель:
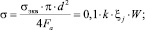
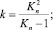
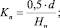
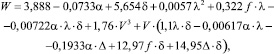
где ξj – коэффициент, характеризующий долю общей осевой нагрузки Fa, воспринимаемую j-м рассматриваемым витком; f – коэффициент трения в пятне контакта; V – координата (0 ≤ V = Y/Hн ≤ 1 + Δ); Δ – относительное смещение точки контакта по высоте витка (Δ = Δн/ Hн).
Адекватность полученной математической модели подтверждена данными экспериментальных исследований напряженного состояния сегмента витка поляризационно-оптическим методом.